2．探索活动

　　 探索活动一：

　　 引导学生思考日常生活中一些判断的含义并组织讨论：

　　 问题1　 当你听到，“小明的身高在班上是中等偏上”，“甲球队队员比乙球队队员更年轻”……你思考过这些话的含义吗?你知道人们是如何做出这些判断的吗?

　　 问题2　 在篮球比赛中，队员的身高是反映球队实力的一个重要指标，如何反映两支球队队员的身高指标?怎样理解“甲球队队员的身高比乙球队队员更高?”

　　 探索活动二：

　　 根据创设的情境，引导学生思考相关的问题，并展开讨论．

　　 探索活动三：

　　 对课本“思考”中小明和小丽的做法展开讨论．目的是给学生搭建从算术平均数到加权平均数过渡的台阶．

1．情境创设

　　 除课本创设的情境外，也可以选取学生熟悉的其他材料作为问题情境．

2．能说出“权”的差异对平均数的影响，算术平均数和加权平均数的联系与区别，并能利用它们解决，-些实际问题，进一步增强统计意识和数学应用的能力．

[教学过程(第一课时)]

1．知道算术平均数和加权平均数的意义，会求-组数据的算术平均数和加权平均数．

6.1 平均数

[教学目标]

2．用尝试求值的方法探索函数的最大值.

1.二次函数的一般形式：；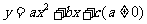

3、已知正方形的边长为x，若边长增加5，求面积y与x的函数表达式．

[例4]如果人民币一年定期储蓄的年利率是x，一年到期后，银行将本金和利息自动按一年定期储蓄转存，到期支取时，银行将扣除利息的20%作为利息税．请你写出两年后支付时的本息和y(元)与年利率x的函数表达式．

[例5]某商场将进价为40元的某种服装按50元售出时，每天可以售出300套．据市场调查发现，这种服装每提高1元售价，销量就减少5套，如果商场将售价定为x，请你得出每天销售利润y与售价的函数表达式．

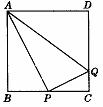
[例6]如图2-1-1，正方形ABCD的边长为4，P是BC边上一点，QP⊥AP交DC于Q，如果BP=x，△ADQ的面积为y，用含x的代数式表示y．

2、　 已知正方形的周长是x，面积为y，求y与x之间的函数表达式．

[例1]　 函数y=(m+2)x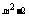+2x－1是二次函数，则m=　　　　 ．

[例2]　 下列函数中是二次函数的有(　　　 )

①y=x+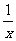；②y=3(x－1)²+2；③y=(x+3)²－2x²；④y=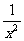+x．

A．1个　　 B．2个　　 C．3个　　 D．4个

[例3]正方形的边长是5，若边长增加x，面积增加y，求y与x之间的函数表达式．

1、　 已知正方形的周长为20，若其边长增加x，面积增加y，求y与x之间的表达式．