6.1 平均数

[教学目标]

4．小结

　　 举例说明算术平均数和加权平均数的区别与联系?

　　 引导学生理解算术平均数实质上是加权平均数的一种特殊情形，即各项的权相等．

　　 某班同学平均身高1.66m，小明身高1.68m，你认为他的身高是中等偏上吗?如果说小明的身高中等偏下，你相信吗?

3．例题教学

　　 根据教学的实际情况，除了课本上的例题外，可考虑选用如下例题：

　　 小凯家上月用于伙食的费用为720元，用于教育的费用为240元，其他费用为1100元．本月小凯家这三项的费用分别增长了9%、30%和6%．小凯家本月的总费用比上月增长的百分数是多少?

　　 小明的算法：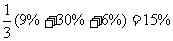

　　 小丽的算法：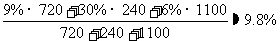

　　 小明和小丽的算法哪一个正确?为什么?

　　 目的在于了解日常生活中很多的“平均”现象并非算术平均，大多数情况应视为加权平均．教师还可以举一些这样的事例，例如，彩票的平均收益，不是各个等次奖金额的算术平均数，而应考虑不同等次奖金的获奖的比例．

2．探索活动

　　 通过课本设计的“讨论”，使学生了解“权”的差异对平均数的影响，认识到“权”的重要性，理解算术平均数和加权平均数的联系与区别．

1．情境创设

　　 除了课本提供的情境外，也可以学生熟悉的计算学期总评成绩作为情境．

　　 在日常生活中，我们经常与平均数打交道，但有时会发现通常计算平均数的方法并不是总是适用的．

　 例如，每学期我们的总评成绩就不是简单地将平时成绩、期中成绩和期末成绩加起来除以3，一般是按3：3：4的比例来计算的．

2．能说出“权”的差异对平均数的影响，算术平均数和加权平均数的联系与区别，并能利用它们解决，-些实际问题，进一步增强统计意识和数学应用的能力．

[教学过程(第二课时)]

1．知道算术平均数和加权平均数的意义，会求-组数据的算术平均数和加权平均数．

6.1 平均数

[教学目标]

4．小结

　　 通过问题情境，体会对数据进行加工处理与描述的必要性，思考日常生活中一些判断的含义与依据，掌握算术平均数的简化算法与公式，培养了计算能力、思维能力和观察能力，发展了统计意识．

3．例题教学

　　 课本没有配置例题，教师可根据实际情况，有必要时可自编例题．在自编例题的教学中，要注意学生表达的条理，书写的规范．