
 (1)一次实验中,硬币两次落地后可能出现几种情况图片来源,百度搜索→硬币.
(1)一次实验中,硬币两次落地后可能出现几种情况图片来源,百度搜索→硬币.
(2)做20次实验,根据实验结果,填写下表.
|
结果 |
正正 |
正反 |
反反 |
|
频数 |
|
|
|
|
频率 |
|
|
|
(3)根据上表,制作相应的频数分布直方图.
(4)经观察,哪种情况发生的频率较大.
(5)实验结果为“正反”的频率是多大.
(6)5个同学结成一组,分别汇总其中两人,三人,四人,五人的实验数据,得到40次,60次,80次,100次的实验结果,将相应数据填入下表。
|
实验次数 |
40次 |
60次 |
80次 |
100次 |
|
“正反”的频数 |
|
|
|
|
|
“正反”的频率 |
|
|
|
|
(7)依上表,绘制相应的折线统计图.
 (8)计算“正反”出现的概率.
(8)计算“正反”出现的概率.
(9)经过以上多次重复实验,所得结果为“正反”的频率与你计算的“正反”的概率是否相近.


“正正” “反反”

“正反”
分别求出每种情况的概率.
(1)小刚做法:通过列表可知,每种情况都出现一次,因此各种情况发生的概率均占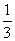 .
.
|
可能出现的情况 |
正正 |
正反 |
反反 |
|
概率 |
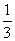 |
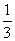 |
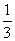 |


小敏的做法:
|
第一枚硬币的可能情况 第二枚硬币的可能情况 |
正 |
反 |
|
正 |
正正 |
反正 |
|
反 |
正反 |
反反 |
通过以上列表,小敏得出:“正正”的情况发生概率为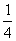 .“正反”的情况发生的概率为
.“正反”的情况发生的概率为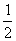 ,“反反”的情况发生的概率为
,“反反”的情况发生的概率为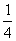 .
.
(1)以上三种做法,你同意哪种,说明你的理由.
 (1)一次实验中,硬币两次落地后可能出现几种情况图片来源,百度搜索→硬币.
(1)一次实验中,硬币两次落地后可能出现几种情况图片来源,百度搜索→硬币.
(2)做20次实验,根据实验结果,填写下表.
|
结果 |
正正 |
正反 |
反反 |
|
频数 |
|
|
|
|
频率 |
|
|
|
(3)根据上表,制作相应的频数分布直方图.
(4)经观察,哪种情况发生的频率较大.
(5)实验结果为“正反”的频率是多大.
(6)5个同学结成一组,分别汇总其中两人,三人,四人,五人的实验数据,得到40次,60次,80次,100次的实验结果,将相应数据填入下表。
|
实验次数 |
40次 |
60次 |
80次 |
100次 |
|
“正反”的频数 |
|
|
|
|
|
“正反”的频率 |
|
|
|
|
(7)依上表,绘制相应的折线统计图.
 (8)计算“正反”出现的概率.
(8)计算“正反”出现的概率.
(9)经过以上多次重复实验,所得结果为“正反”的频率与你计算的“正反”的概率是否相近.
(1)请再回顾一下我们是怎样将复杂的调查转化成模球实验的?
(2)请熟悉你的计算器产生随机数字的操作程序.

4.小结
举例说明算术平均数和加权平均数的区别与联系?
引导学生理解算术平均数实质上是加权平均数的一种特殊情形,即各项的权相等.
某班同学平均身高1.66m,小明身高1.68m,你认为他的身高是中等偏上吗?如果说小明的身高中等偏下,你相信吗?
3.例题教学
根据教学的实际情况,除了课本上的例题外,可考虑选用如下例题:
小凯家上月用于伙食的费用为720元,用于教育的费用为240元,其他费用为1100元.本月小凯家这三项的费用分别增长了9%、30%和6%.小凯家本月的总费用比上月增长的百分数是多少?
小明的算法: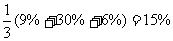
小丽的算法: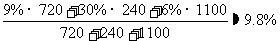
小明和小丽的算法哪一个正确?为什么?
目的在于了解日常生活中很多的“平均”现象并非算术平均,大多数情况应视为加权平均.教师还可以举一些这样的事例,例如,彩票的平均收益,不是各个等次奖金额的算术平均数,而应考虑不同等次奖金的获奖的比例.
2.探索活动
通过课本设计的“讨论”,使学生了解“权”的差异对平均数的影响,认识到“权”的重要性,理解算术平均数和加权平均数的联系与区别.
1.情境创设
除了课本提供的情境外,也可以学生熟悉的计算学期总评成绩作为情境.
在日常生活中,我们经常与平均数打交道,但有时会发现通常计算平均数的方法并不是总是适用的.
例如,每学期我们的总评成绩就不是简单地将平时成绩、期中成绩和期末成绩加起来除以3,一般是按3:3:4的比例来计算的.
2.能说出“权”的差异对平均数的影响,算术平均数和加权平均数的联系与区别,并能利用它们解决,-些实际问题,进一步增强统计意识和数学应用的能力.
[教学过程(第二课时)]
6.1 平均数(2)
[教学目标]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com