
2.发展学生的辩证思维能力.
重点、难点、关键:
1.积极参与数学活动.通过实验提高学生学习数学的兴趣.
1.频率与概率
知识与技能目标:
通过实验.理解当实验次数较大时实验频率稳定于理论概率,并据此估计某一事件发生的概率.
过程与方法目标:
经历实验、统计等活动过程,在活动中进一步发展学生合作交流的意识和能力.
情感态度与价值观目标:
4.想一想
[师]我们在前面估算出了当实验次数很大时,两张牌的牌面数字和等于3的频率约为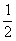 .接着又用树状图计算出了两张牌的牌面数字和等于3的概率也为
.接着又用树状图计算出了两张牌的牌面数字和等于3的概率也为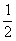 .比较两者之间的关系,你可以发现什么呢?同学们可相互交流意见.
.比较两者之间的关系,你可以发现什么呢?同学们可相互交流意见.
[生]可以发现“实验频率稳定于理论概率”这一结论.
[生]也就是说,当实验次数很大时,两张牌的牌面数字和等于3的频率稳定在相应的概率附近.
[师]很好!由于实验次数很大时,两张牌的牌面数字和等于3的频率稳定在相应的概率附近,因此我们可以通过多次实验,用一个事件发生的频率来估计这一事件发生的概率.
“当实验次数很大时,两张牌的牌面数字和等于3的频率稳定在相心的概率附近”是否意味着。实验次数越大。就越为靠近?应该说.作为一个整体趋势,上述结论是正确的,但也可能会出现这样的情形:增加了几次实验,实验数据与理论概率的差距反而扩大了.同学们可从绘制的折线统计图中发现.
Ⅲ.随堂练习
活动二:
活动课题
利用学生原有的实验数据统计两张牌的牌面数字和为2的频率,进-步体会当实验次数很大时,频率的稳定性及其与概率之间的关系.
活动方式
小组活动,全班讨论交流.
活动步骤
(1)六个同学组成一个小组,根据原来的实验分别汇总其中两人、二人、四人、五人、六人的数据,相应得到实验60次、90次、120次、150次、180次时两张牌的牌面数字和等于2的频率.
(2)根据上面的数据绘制相应的统计图
表,如折线统计图.
(3)根据统计图表估计两张牌的牌面数字和等于2的概率.
(活动完成后,讨论、总结)
[生]由我们组绘制的折线统计图可以发现随着实验次数的增加,实验的频率在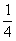 处波动.而且波动越来越小.
处波动.而且波动越来越小.
[生]由此可估计两张牌的牌面数字和等于2的概率为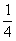 .
.
[师]你能用树状图计算出它的理论概率吗?
[生]可以,如下图:
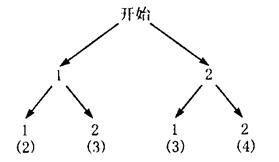
因此,P(两张牌的牌面数字和为2)=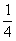 .
.
Ⅳ.课时小结
本节课通过实验、统计等活动,进一步理解“当实验次数很大时,实验频率稳定于理论概率”这一重要的概率思想.
Ⅴ.课后作业
习题6.1
Ⅵ.活动与探究
下列说法正确的是……………( )
A. 某事件发生的概率为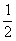 ,这就是说:在两次重复实验中,必有一次发生
,这就是说:在两次重复实验中,必有一次发生
B.一个袋子里有100个球,小明摸了8次,每次都只摸到黑球,没摸到白球,结论:袋子里只有黑色的球
C.两枚一元的硬币同时抛下,可能出现的情形有:①两枚均为正;②两枚均为反;③一正一反,所以出现一正一反的概率是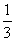
D.全年级有400名同学,一定会有2人同一天过生日
[过程]“当实验次数很大时,实验频率稳定于理论概率”并不意味着,实验次数越大,就越为靠近,应该说,作为一个整体趋势,上述结论是正确的,更不能某某事件的概率为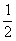 ,在两次重复试验中.就一定有一次发生、因此A不正确,B也不正确
,在两次重复试验中.就一定有一次发生、因此A不正确,B也不正确
而对于C,两枚硬币同时抛下,等可能的情况由树状图可知有四种:
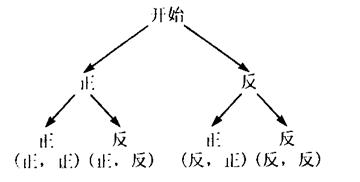
因此,出现一正一反的概率为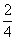 即
即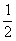 ,对于D,根据抽屉原理可知是正确的.
,对于D,根据抽屉原理可知是正确的.
[结果]应选D.
板书设计
§6.1.1 频率与概率
活动一:
活动目的
活动方式
活动步骤:(1)(2)(3)(4)(5)(6)
活动结果:当实验次数很大时,实验频率稳定于理论概率.
注:对上述结果的正确理解.应该说作为一种整体趋势是正确的.
活动二:
活动目的
活动方式:分组、全班交流讨论.
活动步骤:(1)(2)
活动结果:同上.
3.做-做
[师]你能用我们学过的知识计算出两张牌的牌面数字和为3的概率吗?
[生]每组牌中,每张牌被摸到的可能性是相同的,因此.一次实验中.两张牌的牌面数字的和等可能的情况有:
1+1=2;1+2=3;
2+1=3;2+2=4.
共有四种情况.而和为3的情况有2种,因此,P(两张牌的牌面数字和等于3)= 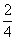 =
=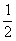 .
.
[生]也可以用树状图来表示,即
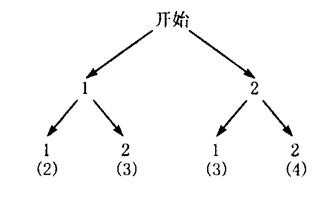
两张牌的牌面数字的和有四种等可能的情况,而两张牌的牌面数字和为3的情况有2次,因此.两张牌的牌面数字的和为3的概率为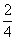 =
=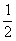 .
.
2.议一议
[师]在上面的实验中,你发现了什么?如果继续增加实验次数呢?与其他小组交流所绘制的图表和发现的结论.
[生]在与各组交流图表的过程中,我发现:在各组的折线统计图中,随着实验次数的增加,频率的“波动”较小了.
[生]随着实验次数的增加,实验结果的差异较小。实验的数据即两张牌的牌面数字和等于3的频率比较稳定.
[生]一个人的实验数据相差可能较大,而多人汇总后的实验数据即两张牌的牌面数字和等于3的频率相差较小.
[师]也就是说,同学们从实验中都能体会到实验次数较大时,实验频率比较稳定.请问同学们估计一下,当实验次数很大时,两张牌的牌面数字和等于3的频率大约是多少?
[生]大约是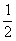 .
.
[师]很好!准能将实验次数更进一步增加呢?越大越好.
[生]可以把全班各组数据集中起来,这样实验次数就会大大增加.
[师]太棒了!“众人拾柴火焰高”,我们集小全班的实验数据,交流合作,可以使实验次数达到一千多次.下面我们汇总全班的实验次数及两张牌的牌面数字和为3的频数,求出两张牌的牌面数字和等于3的频率.
(可让各组一一汇报,然后清同学们自己算出)
[生]约为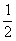 .
.
[师]与你们的估计相近吗?
[生]相近.
1.活动一:
活动课题
通过摸牌活动,探索出“实验次数很大时,实验的频率渐趋稳定”这一规律.
活动方式
分组实验,全班合作交流.
 活动步骤
活动步骤
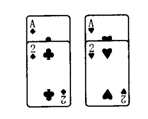
准备两组相同的牌,
每组两张。两张牌的牌
面数字分别是1和2.
从每组牌中各摸出一张,
称为一次实验.
(1)估计一次实验中。两张牌的牌面数字和可能有哪些值?
(2)以同桌为单位,每人做30次实验,根据实验结果填写下面的表格:
|
牌面数字和 |
2 |
3 |
4 |
|
频数 |
|
|
|
|
频率 |
|
|
|
(3)根据上表,制作相应的频数分布直方图.
(4)根据频数分布直方图.估计哪种情况的频率最大?
(5)计算两张牌的牌面数字和等于3的频率是多少?
(6)六个同学组成一组,分别汇总其中两人、三人、四人、五人、六人的实验数据,相应得到实验60次、90次、120次、150次、180次时两张牌的牌面数字之和等于3的频率,填
写下表.并绘制相应的折线统计图.
|
实验次数 |
60 |
90 |
120 |
150 |
180 |
|
两张牌面数字和等于3的频数 |
|
|
|
|
|
|
两张牌面数字和等于3的频率 |
|
|
|
|
|
(在具体实验活动的展开过程中.要力图体现各个步骤的渐次递进.(1)在一次实验中,两张牌的牌面数字和可能为2,3,4:(2)学生根据自己的实验结果如实填写实验数据;(3)制作相应的频数分布直方图,一方面为了复习巩固八年级下册有关频数、频率的知识,同时也便于学生更为直观地获得(4)的结论;(4)一般而言,学生通过实验以及上面(2)(3)的图表容易猜想两张牌的牌面数字和为3的频率最大.理论上.两张牌的牌面数字和为2,3,4的概率依次为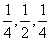 ,应该说,经过30次实验,学生基本能够猜想两张牌的牌面数字和为3的频率最大.当然,这里一定要保证实验的次数,如果实验次数太少,结论可能会有较大出入;(5)有了(4)中的结沦.自然过渡到研究其频率的大小.当然,两张牌的牌面数字和等于3的频率因各组实验结果而异.正是有了学生结论的差异性,才顺理成章地展开问题(6),汇总组内每人的实验数据;(6)目的在于通过逐步汇总学生的实验数据,得到实验60次、90次、120次、150次、180次时的频率.并绘制相应的折线统计图,从而动态地研究频率随着实验次数的变化而变化的情况)
,应该说,经过30次实验,学生基本能够猜想两张牌的牌面数字和为3的频率最大.当然,这里一定要保证实验的次数,如果实验次数太少,结论可能会有较大出入;(5)有了(4)中的结沦.自然过渡到研究其频率的大小.当然,两张牌的牌面数字和等于3的频率因各组实验结果而异.正是有了学生结论的差异性,才顺理成章地展开问题(6),汇总组内每人的实验数据;(6)目的在于通过逐步汇总学生的实验数据,得到实验60次、90次、120次、150次、180次时的频率.并绘制相应的折线统计图,从而动态地研究频率随着实验次数的变化而变化的情况)
2.在活动中发展学生的合作交流意识和能力.
教学难点
辩证地理解当实验次数较大时,实验频率稳定于理沦概率.
教学方法
实验--交流合作法.
教具准备
每组准备两组相同的牌,每组牌都有两张;
多媒体演示:
教学过程
Ⅰ.创设问题情境,引入新课
[师]我们在七年级时,曾用掷硬币的方法决定小明和小丽谁去看周末的电影:任意掷一枚均匀的硬币.如果正面朝上,小丽去;如果反面朝上,小明去.这样决定对双方公平吗?
[生]公平!因为我们做过这样的试验,历史上的数学家也做过掷硬币的实验,经过实验发现当次数很大时,任意掷一枚硬币.会出现两种可能的结果:正面朝上、反面朝上.
这两种结果出现的可能性相同.都是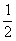
[师]很好!我们再来看一个问题:任意掷一枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).“6”朝上的概率是多少?
[生]任意掷一枚均匀的小立方体,所有可能出现的结果有6种:“1”朝上,“2”朝上。
“3”朝上,“4”朝上,“5”朝上,“6”朝上,每种结果出现的概率都相等,其中“6”朝上的结果只有一种,因此P(“6”朝上)=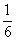 .
.
[师]上面两个游戏涉及的是一步实验.如果是连续掷两次均匀的硬币。会出现几种等可能的结果.出现“一正一反”的概率为多少呢?如果将上面均匀的小立方体也连续掷两次,会出现几种等可能的结果,两次总数都是偶数的概率为多少呢?从这一节开始我们将进一步学习概率的有关知识.
我们用实验的方法估计出了任意掷一枚硬币“正面朝上”和“反面朝上”的概率.同样
的我们也可以通过实验活动.估计较复杂事件的概率.
Ⅱ.分组实验,进一步理解当实验次数较大时,实验频率稳定于理论概率.
1.通过实验.理解当实验次数较大时。实验频率稳定于理论概率.并据此估计某一事件发生的概率.
2.发展学生的辩证思维能力.
教学重点
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com