
1. 什么是有序数对?
2. 培养用数学的意识.
重点
有序数对及平面内确定点的方法.
活动1 感受生活中的数学
问题:
⑴在电影院内如何找到电影票上所指的位置?
⑵在电影票上,“6排3号”与“3排6号”中的“6”的含义有什么不同?
⑶如果将“8排3号”简记作(8,3),那么“3排8号”如何表示?(5,6)表示什么含义?
活动2 有序数对
问题:
1. 理解有序数对的应用意义,了解平面上确定点的常用方法
6.1.1有序数对 学案
学习目标
将各组的数据集中起来,求出两张牌的牌面数字和等于3的频率,它与你们的估计相近吗?
结论:我们可以通过多次实验,用一个事件发生的频率来估计这一事件发生的概率.
(1) 在上面的实验中,你发现了什么?如果继续增加实验次数呢?与其他小组交流所绘制的图表和发现的结论
(2) 当实验次数很大的时候,你估计两张牌的牌面数字和等于3的频率大约是多少?你是怎么估计的?
2、 实验二:准备两组相同的牌,每组两张,两张牌的牌面数字分别是1和2.从每组牌中各摸出一张,称为一次实验.
(1) 一次实验中两张牌的牌面数字和可能有哪些值?
(2) 每人做30次实验,依次记录每次摸得的牌面数字,并根据实验结果填写下面的表格:
|
牌面数字和 |
2 |
3 |
4 |
|
频数 |
|
|
|
|
频率 |
|
|
|
(3) 根据上表,制作相应的频数分布直方图
(4) 你认为哪种情况的频率最大?
(5) 两张牌的牌面数字和等于3的频率是多少?
(6) 汇总各个小组的数据,填写下表,并绘制相应的的频率折线统计图
|
实验次数 |
60 |
90 |
120 |
150 |
180 |
|
两张牌的牌面数字和等于3的频数 |
|
|
|
|
|
|
两张牌的牌面数字和等于3的频率 |
|
|
|
|
|
1、实验一:准备20张大小相同的卡片,上面分别写好1至20的数字,然后将卡片放在袋子里搅匀,每次从袋中抽出一张卡片,记录结果,然后放回搅匀再抽.
(1) 将实验结果填入下表:
|
实验次数 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
|
出现5的倍数的频数 |
|
|
|
|
|
|
|
|
|
|
|
出现5的倍数的频率 |
|
|
|
|
|
|
|
|
|
|
(2) 根据上表中的数据绘制频率折线图
(3) 从实验数据中可以发现什么规律?
(4) 频率随着实验次数的增加,稳定于什么值?
(5) 从袋中抽出一张卡片是5的倍数的概率是多少?
2.鼓励学生积极参与数学活动,进一步提高学习数学的信心.
教学重点
进一步经历用树状图、列表法计算随机事件发生的概率.
教学难点
正确地利用列表法计算随机事件发生的概率.
教学方法
巩固复习
教具准备
多媒体演示
教学过程
Ⅰ.创设情境,引入新课
[师]上一节,我们用列表法求出掷两次骰子,点数和为6的概率,下面请同学们利用列大法.求出掷两枚骰子:(多媒体演示)
(1)“点数和为12点”的概率;
(2)“点数和至少是9点”的概率;
(3)“两颗骰子点数相同”的慨率;
(4)“两颗骰子的点数都是偶数”的概率;
(5)“点数和为1点”的概率;
(6)“点数和小于13点”的概率.
[师生共析]掷两枚骰子,所有等可能的情况列表如下:
 第二点 第二点点数 第一次 点数 |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
(1,1) |
(1,2) |
(1,3) |
(1,4) |
(1,5) |
(1,6) |
|
2 |
(2,1) |
(2,2) |
(2,3) |
(2,4) |
(2,5) |
(2,6) |
|
3 |
(3,1) |
(3,2) |
(3,3) |
(3,4) |
(3,5) |
(3,6) |
|
4 |
(4,1) |
(4,2) |
(4,3) |
(4,4) |
(4,5) |
(4,6) |
|
5 |
(5,1) |
(5,2) |
(5,3) |
(5,4) |
(5,5) |
(5,6) |
|
6 |
(6,1) |
(6,2) |
(6,3) |
(6,4) |
(6,5) |
(6,6) |
根据上表可知,共有36个等可能的基本事件,(1)其是点数和为12点的有(6.6)一种.因此“点数和为12点”的概率为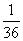 ;
;
(2)总点数至少是9点的有(3,6),(4,5),(5,4),(6,3),(6,4),(6,5),(6,6),(5,5),(5,6),(4,6)十种情况,因此,“点数和至少是9点”概率为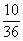 即
即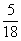 ;
;
(3)两颗骰子的点数相同的有(1,1).(2,2),(3,3),(4,4),(5,5),(6,6)六种情况,因此,“两颗骰子点数相同”的概率为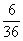 即
即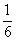 ;
;
(4)两颗骰子的点数都为偶数的有(2,2),(2,4),(2,6).(2,4),(4,4),(6,4),(2,6),(4,6),(6,6)共九种情况.因此,“两颗骰子的”
(5)点数和为1的情况没有发生,因此,“点数和为1点”的概率为即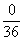 即0;
即0;
(6)点数和小于13的情况共有36种,因此,“点数和小于13点”的概率为 =1.
=1.
[生]我们在七年级学习过随机事件,必然事件,不可能事件,由上面的计算更进一步验证上面:随机事件的概率是大于零且小于1的;必然事件的概率为1;不可能事件的概率为0.
我们下面再来看一个题目,你能刚树状图、列表法两种方法解决吗?
Ⅱ.巩固、练习树状图和列表法
多媒体演示
[例题]一枚硬币和一枚骰子一起掷,求:
(1)“硬币出现正面,且骰子出现6点”的概率;
(2)“硬币出现正面,或骰子出现6点”的概率.
[生]由于硬币出现正面、反面的可能性相同,骰子出现1,2,3,4,5,6点的可能性也相同,一枚硬币与一颗骰子同时掷出现的所有等可能的情况用树状图表示如下:
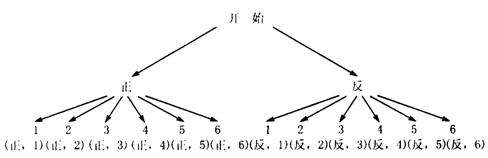
(1)硬币出现正面且骰子出现6点的情况有(正,6),因此,“硬币出现正面且骰子出现6点”的概率为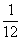 ;
;
(2)硬币出现正面或骰子出现6点的情况有(正,1),(正,2),(正,3),(正,4),(正,5),(正,6).(反,6),因此,“硬币山现正面或骰子出现6点”的概率为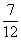 .
.
[生]用列表法,可得
 骰子 骰子硬币 |
1 |
2 |
3 |
4 |
5 |
6 |
|
正面 |
(正,1) |
(正,2) |
(正,3) |
(正,4) |
(正,5) |
(正,6) |
|
反面 |
(反,1) |
(反,2) |
(反,3) |
(反,4) |
(反,5) |
(反,6) |
共有12种等可能情况.(1)“硬币出现正面,且骰子出现6点”的概率为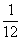 ;(2“硬币出现正面或骰子出现6点”的概率为
;(2“硬币出现正面或骰子出现6点”的概率为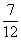 .
.
Ⅲ.随堂练习
多媒体演示:
用如图所示的转盘进行“配紫色”游戏.
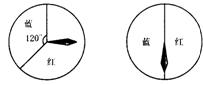
小颖制作了下表,并据此求出游戏者获胜的概率为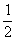 ;
;
|
|
红色 |
蓝色 |
|
红色 |
(红,红) |
(红,蓝) |
|
蓝色 |
(蓝,红) |
(蓝,蓝) |
小亮则先把左边转盘的红色区域等分成2份,分别记作“红色1”“红色2”,然后制作了下表,据此求出游戏者获胜的概率也是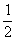 .
.
|
|
红色 |
蓝色 |
|
红色1 |
(红1,红) |
(红1,蓝) |
|
红色2 |
(红2,红) |
(红2,蓝) |
|
蓝色 |
(蓝,红) |
(蓝,蓝) |
你认为谁做得对?说说你的理由.
[生]小颖的做法不正确,小亮的做法正确.因为左边的转盘中红色部分和蓝色部分的面积不同,因而指针落在两个区域的可能性不同.而用列表法求随机事件发生的概率时,应注意各种情况出现的可能性务必相同.而小亮的做法把左边转盘中的红色区域等分成2份,分别记作“红色1”“红色2”,保证了左边转盘中指针落在“蓝色区域”“红色1”“红色2”三个区域的等可能性,因此是正确的.
Ⅳ.课时小结
本节课我们继续复习巩固了用树状图和列表法求随机事件的概率,进一步加深了用列表法求概率时应注意各种情况出现的可能性务必相同.
Ⅴ.课后作业
习题6.2 第2题
Ⅵ.活动与探究
掷三枚硬币,求:
(1)“至少有一个硬币是正面”的概率;
(2)“三枚硬币都是反面”的概率.
[过程]画掷三枚硬币的树状图要有两次分叉.
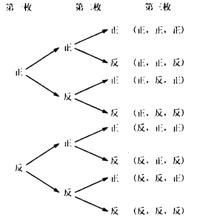
从树状图可知共有8个等可能的基本事件.并且可知“至少有一枚硬币是正面”共有7个基本事件;“三枚都是反面”有1个基本事件.
[结果](1)“至少有一枚硬币是正面”的概率为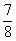 ;
;
(2)“三枚都是反面”的概率为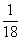
板书设计
§6.1.3 频率与概率(三)
[例1]掷两枚均匀的骰子.
解:(1)“点数和为12点”的概率为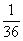 ;
;
(2)“点数和至少是9点”的概率为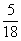 ;
;
(3)“两颗骰子点数相同”的概率为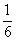 ;
;
(4)“点数都为偶数”的概率为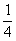 ;
;
(5)“点数和为1”的概率为0;
(6)“总数和小于13”的概率为1.
[例2]一枚硬币和一枚骰子一起掷.求:
(1)“硬币出现正面,且骰子出现6点”的概率;
(2)“硬币出现正面,或骰子出现6点”的概率;
1.鼓励学生思维的多样性,发展学生的创新意识.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com