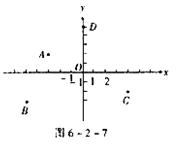
1.如图6-2-7，某城市有4个牛奶供应站A(-3,2)、B(-5,-3)、C(4,-2)、D(0,5),现在建一个牛奶供应总站，总站建在AC与BD的交叉点上，你能确定总站的位置吗？

2.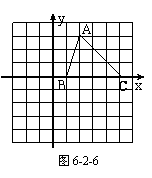如图6-2-6，△ABC沿x轴向作平移4个单位后得到△A₁B₁C₁，再作△A₁B₁C₁，关于x轴的轴对称图形，比较变化后的三角形的三个顶点的坐标有什么变化.

1.如图6-2-5时效应所在学校的平面示意图，小英可以如何

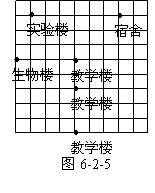描述他所住的宿舍位置呢？

2.人们给电脑屏幕上的点也建立了坐标系，如果电脑屏幕

左下方的点是(0,0)右上方的点的坐标是(720,600),要在屏幕

的中央画一个点，此点的坐标是　　　　 .

1.如图6-2-4是公园平面示意图，试借助刻度尺、量角器解决下列问题并填空：荷花池

在大门的北偏西　　　 度的方向上，到大门的距离为　　 厘米；马戏团在九曲桥的　　　　 度的方向上，到九曲桥的距离为　　　 厘米.

6.2　 坐标方法的简单应用

你喜欢旅游吗？给你一张风景区景点图，你会识图吗？你能用坐标准确地表示景点的位置吗？学习了本节知识，你就明白该怎么做啦！

[例1]如图6-2-1，某城市A地和B地之间经常有车辆来往，H地和D地间也经常有车辆来往.建立如图所示的直角坐标系，四地的坐标为：A(-3,2),D(1,1),H(-5,-3),B(-1,-4),拟建一座加油站，那么加油站建立在哪里对大家都方便，是给出具体的位置.

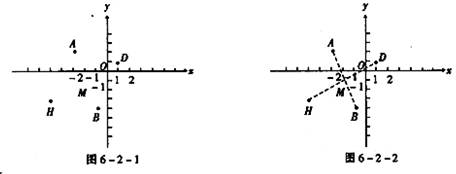
[点拨]关键是加油站建在何处对大家都方便，也就是大家都加油站距离较近，显然应建在两条道路的交叉点上较方便.

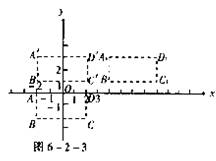[答案]加油站应建在点M(-2,-1)处，因为此处是道路与道路的交叉口，加油站建在此处对两条道路上的车加油都方便，结果如图6-2-2所示

　 [例2]图6-2-3中，矩形ABCD沿y轴向上平移3个单位

后，得到矩形A′B′C′D′.四个顶点的坐标有什么变化呢？

若矩形A′B′C′D′再沿x轴向右平移6个单位后，得到的

矩形A₁B₁C₁D₁,四个顶点的坐标有什么变化呢？

　 [点拨]关键是搞清平移方向.若沿x轴平移，则横坐标

变化而纵坐标不变；若沿y轴平移，则纵坐标变化而横坐标不变.

[答案]矩形ABCD的四个顶点的坐标是A(-2,0),B(-2,-2),C(2,-2),D(2,0);沿y轴平移后的矩形A′B′C′D′四个顶点的坐标是A′(-2,3),B′(-2,1),C′(2,1), D′(2,3);沿x轴平移后的矩形A₁B₁C₁D₁,四个顶点的坐标是A₁(4,3),B₁(4,1),C₁(8,1),D₁(8,3).

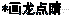
1°的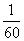为1分，记作“1′”即1°=60′；

1′的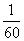为1秒，记作“1″”即1′=60″；

讲解例一：

(1)1.45°等于多少分？等于多少秒？

(2)1800″等于多少分？等于多少度？

注意：例一的问法与“1805″等于多少分多少秒？”的区别。

练习：

(1)0.　　　　 25°等于多少分？等于多少秒？

(2)2700″等于多少分？等于多少度？

(3)3716″等于多少度多少分多少秒？

　 课后思考题：3点45分时，时针与分针成多少度角？

小　　 结： (1)角的表示法；

(2)度、分、秒、的换算。

作　　 业： 课本P130 习题1、3

教学后记：学生对于这堂课中的角度的表示法掌握很好，度与分、分与秒、秒与度之间的换算还是掌握的可以，但是对于练习的第三小题这样的题目就有点理解不够的现象，需要加强。

①∠ABC　 B点是表示角的顶点,必须放在表示法的字母中间.

②∠1　　 用自然数字表示角,要在角的顶点处标上数字.

③∠B　　 在不引起混乱的情况下可以用单个字母(角的顶点)表示角.

④∠α　　 用希腊字母表示角,要在角的顶点处标上希腊字母.

　 练习:课本P127 做一做

　　　　 以地图上的城市之间的夹角为背景,复习角的度量,巩固角的符号表示.

　 　　　接着要求学生用量角器测量上述角的度数,与同伴交流自己的量法与读法.

6.2角(2)

题目 6.2角(2) 教学目标 会利用三角尺、圆规、量角器、直尺等画图工具画一个角等于已知角 在操作活动中理解角平分线的概念，并会进行简单的计算 教学重点 利用绘图工具画一个角等于已知角 教学难点 尺规作图画一个角等于已知角 理解角平分线的概念 教学方法 引导发现式 教学工具 三角尺、圆规、量角器 教学内容 教师活动 学生活动

一些特殊的角度我们可以用一副三角尺画出 例如∠AOB=45°+30°＝75° ∠AOB=45°－30°＝15° 　 　 　 　 说明：0°到180°之间的所有15°的整数倍角都可以用三角尺画出 用量角器可以画出0°到180°之间任意角度 尺规作图画一个角等于已知角 1.　　　 以点O为圆心，任意长为半径用圆规画弧，分别交OA、OB于点C、D 2.　　　 任意画一点O画射线OA，以点O为圆心，OC长为半径画弧CE，交OA于点C 3.　　　 以点C为圆心，CD长为半径画弧，交弧CE于点D 4.　　　 B 　 过点D作射线OB，∠AOB就是与∠AOB相等的角 O 　 OC将∠AOB分成相等的两部分，OC就是∠AOB的角平分线 我们还可以得到： 如果OC是∠AOB的角平分线 则∠AOC＝∠BOC＝∠AOB 反过来如果∠AOC＝∠BOC或者∠AOC＝∠AOB，　 ∠BOC＝∠AOB 则OC是∠AOB的角平分线 O 　 例 　 ∠AOD＝80°，OB是∠AOC的角平分线， ∠AOB＝30°试求∠AOC、∠COD的度数 解：∠AOC＝2∠AOB＝2×30°＝60° ∠COD＝∠AOD－∠AOC=80°－60°＝20° 练习： P208 1、2 作业： P209 3、4

1°的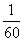为1分，记作“1′”即1°=60′；

1′的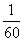为1秒，记作“1″”即1′=60″；

讲解例一：

(1)1.45°等于多少分？等于多少秒？

(2)1800″等于多少分？等于多少度？

注意：例一的问法与“1805″等于多少分多少秒？”的区别。

练习：

(1)0.　　　　 25°等于多少分？等于多少秒？

(2)2700″等于多少分？等于多少度？

(3)3716″等于多少度多少分多少秒？

　 课后思考题：3点45分时，时针与分针成多少度角？

小　　 结： (1)角的表示法；

(2)度、分、秒、的换算。

作　　 业： 课本P130 习题1、3

教学后记：学生对于这堂课中的角度的表示法掌握很好，度与分、分与秒、秒与度之间的换算还是掌握的可以，但是对于练习的第三小题这样的题目就有点理解不够的现象，需要加强。