
1.3 应用:请每一位同学选择一个游玩的景点,然后同座位的同学用坐标相互报告自己的位置,看对方能否准确找到?
[通过这一活动:①可以起到及时巩固的作用;②在同学之间相互帮助、相互评价中,培养学生合作意识与交流能力。]
[活动2] 室内寻宝
1.2 探究:①若小明小华都在温峡水库,应该怎样报告自己的位置老师才明白?②你能再换一个坐标系报告吗?
本节课主要开展三个活动
[活动1] 报告位置
1.1 创设情境:为吸引学生注意力,并产生一种亲切感,课件演示老师和同学们即将游玩的钟祥部分旅游景点,并显示各景点位置的平面示意图,顺势提出问题:游玩中,小明、小华走散了,他俩赶紧用电话向老师报告位置,小明说:“老师,我们这里坐标为(200,200)”,小华说:“不对,我们这里坐标为(0,300)。
想一想:①他们在同一个位置,为什么坐标不同呢?(实际上他们说的坐标都对。)
②老师知道他们在哪个景点吗?为什么?
[通过这一问题的创设,意在与学生已有认识结构之间产生内部矛盾冲突,从而激起探索欲望。]
针对本课教学内容和目标,我以“启发探究式”教学为主,不断创设与实际生活紧密相连的、新颖有趣的并富有挑战性问题情境激发学生,引导学生探究解决问题的办法。让学生在参与丰富多彩的活动中,操作、观察、交流、感悟,老师则在活动中充分发挥组织者、参与者、引导者的作用,从而通过师生有效的数学活动,完成本课教学目标。
准备工作:课前学生按6×11的方阵坐好,并下发给学生操作用的方格纸、塑料花,四边形模型。
3、情感与态度目标:感受数学在日常生活中的广泛应用,体会与他人合作交流的重要性。
2、过程与方法目标:经历“问题情境-建立坐标系模型-解释与应用”的过程,体验数是描述现实世界的重要手段,提高分析问题、解决问题的能力。
1、知识与技能目标:巩固由坐标描点、由点写坐标的技能,掌握用坐标表示物体位置的方法。
2、重难点及成因分析
由以上分析我把重点确定为:能应用坐标法解决实际问题,培养学生的应用意识。由于学生对坐标法的应用还不熟练,能力还不够,所以我把本课的难点确定为:由实际问题转化为数学问题,并能根据实际情况建立适当的坐标系。
2.陈群同学要在电话中告诉同学如图6-2-8所示的图形,为了描述清楚,它使用了与本节有关的知识,你能猜到他用的什么方法吗?请详细叙述他的方法. 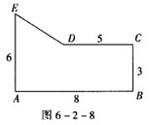

小华去某地考察环境污染问题,并且事先知道下面的信息:
①“悠悠日用化工品厂”在她现在所在地的北偏东300、距离此处3km的地方;
②“加加调味品厂”在她现在所在地的北偏西450、距离此处2.4km的地方;
③“幸福水枯”在她现在所在地的南偏东270、距离此处1.5km的地方,根据这些信息,请建立直角坐标系,帮助小华完成这张表示各处位置的简图
 如图6-2-9中的平行四边形ABCD做下列运动,画出相应的图形,指出四个顶点的坐标发生的变化.
如图6-2-9中的平行四边形ABCD做下列运动,画出相应的图形,指出四个顶点的坐标发生的变化.
(1)沿y轴正向平移2个单位;
(2)关于y轴对称;
(3)以点A为中心,将平行四边形ABCD旋转1800.

平面上建立直角坐标系的木的使用(x,y)去表示点的位置.其实“坐标”也就是坐标标记
的意思.平面上除建立直角坐标系及点的位置外,还可建立各种各样的坐标系来标记点的位置,例如:极坐标系.
如果知道了一点M相对于以顶点O的距离和方向,那么这个点的位置就被惟一确定了,这就是说,我们可用角度和距离来确定平面上的点的相对位置.
在平面内取一个顶点O叫做极点,引一条射线OX,叫做极轴,在选定一个长度单位和角度的正方向(通常取逆时针方向).对于平面内任一点M,用ρ表示线段OM的长度,θ表示从OX到OM的角度,ρ叫做点M的极径,θ叫做点M的极角,(注:θ用弧度制,1800=π,900=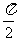 ,300=
,300= ,即10=
,即10= 弧度),有序数对(ρ,θ)就叫做点M的极坐标.这样建立的坐标系叫做极坐标系.极坐标为ρ,θ的点M,可表示为M(ρ,θ).建立极坐标系后,给定ρ和θ,就可以在平面内惟一确定一点M.
弧度),有序数对(ρ,θ)就叫做点M的极坐标.这样建立的坐标系叫做极坐标系.极坐标为ρ,θ的点M,可表示为M(ρ,θ).建立极坐标系后,给定ρ和θ,就可以在平面内惟一确定一点M.
问题:在直角坐标系xOy中,点A、B的坐标为:A(0,3)、B(4,0),若以O为极点,Ox为极轴,你能写出点A、B的极坐标吗?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com