教材第58页练习；习题6．2中第1、2、4题．

展示问题：教材第56页图．

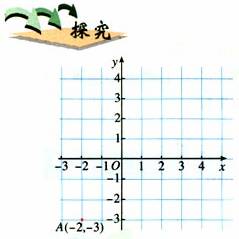
(1)如图将点A(－2，－3)向右平移5个单位长度，得到点A₁，在图上标出它的坐标，把点A向上平移4个单位长度呢？

(2)把点A向左或向下平移4个单位长度，观察他们的变化，你能从中发现什么规律吗？

(3)再找几个点，对他们进行平移，观察他们的坐标是否按你发现的规律变化？

规律：在平面直角坐标系中，将点(x，y)向右(或左)平移a个单位长度，可以得到对应点(x+a，y)(或(　　　 ，　　　 ))；将点(x，y)向上(或下)平移b个单位长度，可以得到对应点(x，y+b)(或(　　　 ，　　　 ))．

教师说明：对一个图形进行平移，这个图形上所有点的坐标都要发生相应的变化；反过来，从图形上的点的坐标的某种变化，我们也可以看出对这个图形进行了怎样的平移．

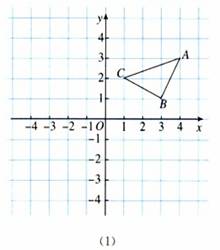
例　 如图(1)，三角形ABC三个顶点坐标分别是A(4，3)，B(3，1)，C(1，2)．

(1)将三角形ABC三个顶点的横坐标后减去6，纵坐标不变，分别得到点A₁、B₁、C₁，依次连接A₁、B₁、C₁各点，所得三角形A₁B₁C₁与三角形ABC的大小、形状和位置上有什么关系？

(2)将三角形ABC三个顶点的纵坐标都减去5，横坐标不变，分别得到点A₂、B₂、C₂，依次连接A₂、B₂、C₂各点，所得三角形A₂B₂C₂与三角形ABC的大小、形状和位置上有什么关系？

引导学生动手操作，按要求画出图形后，解答此例题．

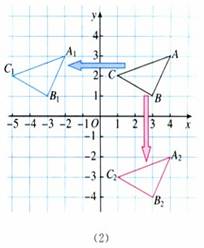
解：如图(2)，所得三角形A₁B₁C₁与三角形ABC的大小、形状完全相同，三角形A₁B₁C₁可以看作将三角形ABC向左平移6个单位长度得到．类似地，三角形A₂B₂C₂与三角形ABC的大小、形状完全相同，它可以看作将三角形ABC向下平移5个单位长度得到．

思考题：

由学生动手画图并解答．

归纳：

上节课我们学习了用坐标表示地理位置，本节课我们继续研究坐标方法的另一个应用．

关于教材的处理

教学应以学生的发展为本，教材中的两个活动对学生来说已较为熟悉，较为简单，不太容易激起学生探索的兴趣与热情，当然也就不能很好培养学生的应用意识，培养应用意识要有一个比较大但又贴近学生身边的实际问题，这个问题对学生来说要富有进行探索和思考的空间，要富有新颖性和挑战性，使学生既感觉到一种联系，但又感觉到一种距离且需综合运用所学知识才能解决。因此，我把教材的活动2作为课外作业，改编了活动1，增添了“室内寻宝”、“电话传图”两个活动，我相信这学生应用意识提高需要这样思维含量高的且有价值的问题。

3.3　 应用：请设计一个简单而有趣的图案(老师可提供参考图案，学生可采用)，按照刚才方法奇数排和偶数排的同学相互传递，看看他人能否收到你的图形？

图形传递成功后的学生到前面展示自己的成果，在老师和同学们的一片肯定与赞扬声中，再次感受到成功的欢乐。

[本环节的活动目的是：培养学生的创新意识和动手能力，同时给学生提供一个自我展示，自我表现的机会，从而增强学生学好数学的信心。]

小结

此阶段教师引导学生着重对活动过程中的体验、感受、认识、收获等进行总结和反思，通过反思，让学生体会到坐标在日常生活中的广泛应用，获得一些解决问题的方法与经验，增强学好数学的信心。

最后老师以问题的形式进行画龙点睛式总结：在实际问题中遇到什么情况时，可用坐标法解决？怎样用坐标法解决？你能再举一些用坐标法解决的实例吗？

作业布置：收集一些校园或自己家附近有代表性的建筑，绘制出相关的平面分布图。

3.2 探究：此问题对学生来说确有一定难度：一是情景新，没有前面“报告位置”、“室内寻宝”两个活动中明显暗示用坐标法解决的痕迹；二是图形比较复杂，影响了学生的观察与联想。为此，我首先简化图形，若学生还是找不到传递的办法，可暗示：小菲传递的是一个组数据，在这个暗示下，学生可能猜想出两种办法：①传递四条边的长度；②传递四个顶点的坐标。然后组织学生讨论第一种办法，让学生拿出准备好的四边形、操作、观察、讨论、发现：已知四条边的长度，并不能确定四边形的形状，因为它的四边还可以动，四个顶点位置也可以动，对方显然无法画出你的图形。这样就否定了第一种办法，但悟出解决问题的关键是：如何让对方准确地画出四个顶点的位置，于是学生不难明白第二种方法正确性，因为学生知道：用坐标可以准确表示点的位置，至此问题基本解决。接下来的具体传递过程由学生完成：首先建立平面直角坐标系，写出点的坐标，然后请一位同学扮演小菲用电话传递(传递时，不仅要说明点的坐标，还要说明如何连结各点)，其他学生在方格纸上描点画出图形。同法传递三角形，对方就准确无误的画出了船的图案。

[设计意图：①让学生经历猜想与探索的过程，培养学生创造性用坐标法解决问题的能力，从而发展学生的应用意识。②让学生初步的感受到坐标系是勾通图形与数量之间关系的桥梁，渗透数形结合的思想。]

3.1 问题情境：小菲非常关心北京2008年奥运，特为奥运会设计一个船的图案“　　 ”，正准备给北京方面发个传真，不巧，停电了，怎么办？小菲灵机一动，在图上比比画画一翻，很快用电话将图案准确无误地传到北京，你知道小菲用得是什么办法吗？

2.3　 应用：作为本活动的延伸，接下来请每个同学记下自己所在位置的坐标，老师让坐标出现在屏幕上的同学举起手，拿起花束，其它同学观察所组成的图案，这意在回应本章开篇提到的建国50周年庆典活动中的背景图案是如何组成的？从而丰富学生用数学的体验。

[活动3]　 电话传图

2.2 　探究:开始学生可能凭直觉找，速度慢，即使找着，也不一定敢确认，老师应及时提醒，有没有又快又准的办法呢？促使学生想到：要确定宝物的准确位置，必须先建立平面直角坐标系这个模型。怎样找坐标系？放手让学生讨论，给学生提供充足的探索和思考的空间，老师只需在必要时给予点拨。

点拨一：仔细观察甲乙两同学坐标有何特点？学生不难发现两坐标关于y轴对称，于是y轴被确定。

点拨二：请再仔细观察甲、乙两同学的坐标，你有何新的发现？即发现第一排同学的纵坐标都为3，进而推算第二排、第三排、第四排的纵坐标，学生不难悟出x轴在第四排上，因为只有x轴上点的纵坐标为0。从而在学生交流讨论，老师点拨引导中突破了难点。

坐标系建好后，学生很快找到宝藏，为使学生更强烈感受到坐标系的作用，不妨再换几个藏宝地点让学生找。

[设计意图：①使学生在活动1的基础上进一步体会平面直角坐标系在确定物体位置中的作用，突出本课重点；②在寻找坐标系过程中，培养学生观察推理能力、交流能力以及综合运用所学的知识解决问题的能力。]

2.1创设情景：已知第一排甲同学已知第一排甲同学坐标为(－2，3)，乙同学坐标为(2，3)，藏宝地点的坐标为(－3，－1)，你知道宝物藏在哪位同学的座位下吗？谁先找到，宝物归谁。