如图：三角形ABC的三个顶点坐标分别为A(1，1)，B(3，1)，C(4,3)，把三角形ABC向左(或向上)平移3个单位后，顶点A、B、C的坐标分别为多少？二、探究新知：

1、探究：把三角形ABC向左(或向上)平移3个单位，相当于把三角形ABC的三个顶点A(1,1)，B(3，1)，C(4，3)分别向作(或向上)平移了3个单位得到A₁、B₁、C₁，此时这三个点的坐标分别是多少？

教材第59页第3题．

教材第58页练习；习题6．2中第1、2、4题．

展示问题：教材第56页图．

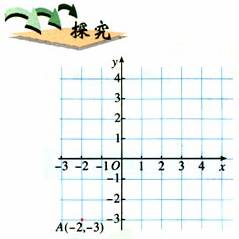
(1)如图将点A(－2，－3)向右平移5个单位长度，得到点A₁，在图上标出它的坐标，把点A向上平移4个单位长度呢？

(2)把点A向左或向下平移4个单位长度，观察他们的变化，你能从中发现什么规律吗？

(3)再找几个点，对他们进行平移，观察他们的坐标是否按你发现的规律变化？

规律：在平面直角坐标系中，将点(x，y)向右(或左)平移a个单位长度，可以得到对应点(x+a，y)(或(　　　 ，　　　 ))；将点(x，y)向上(或下)平移b个单位长度，可以得到对应点(x，y+b)(或(　　　 ，　　　 ))．

教师说明：对一个图形进行平移，这个图形上所有点的坐标都要发生相应的变化；反过来，从图形上的点的坐标的某种变化，我们也可以看出对这个图形进行了怎样的平移．

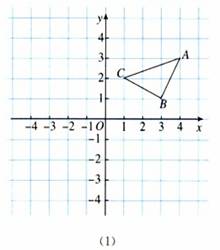
例　 如图(1)，三角形ABC三个顶点坐标分别是A(4，3)，B(3，1)，C(1，2)．

(1)将三角形ABC三个顶点的横坐标后减去6，纵坐标不变，分别得到点A₁、B₁、C₁，依次连接A₁、B₁、C₁各点，所得三角形A₁B₁C₁与三角形ABC的大小、形状和位置上有什么关系？

(2)将三角形ABC三个顶点的纵坐标都减去5，横坐标不变，分别得到点A₂、B₂、C₂，依次连接A₂、B₂、C₂各点，所得三角形A₂B₂C₂与三角形ABC的大小、形状和位置上有什么关系？

引导学生动手操作，按要求画出图形后，解答此例题．

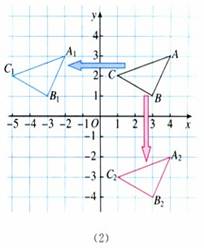
解：如图(2)，所得三角形A₁B₁C₁与三角形ABC的大小、形状完全相同，三角形A₁B₁C₁可以看作将三角形ABC向左平移6个单位长度得到．类似地，三角形A₂B₂C₂与三角形ABC的大小、形状完全相同，它可以看作将三角形ABC向下平移5个单位长度得到．

思考题：

由学生动手画图并解答．

归纳：

上节课我们学习了用坐标表示地理位置，本节课我们继续研究坐标方法的另一个应用．

教材第59页第3题．

教材第58页练习；习题6．2中第1、2、4题．

展示问题：教材第56页图．

(1)如图将点A(－2，－3)向右平移5个单位长度，得到点A₁，在图上标出它的坐标，把点A向上平移4个单位长度呢？

(2)把点A向左或向下平移4个单位长度，观察他们的变化，你能从中发现什么规律吗？

(3)再找几个点，对他们进行平移，观察他们的坐标是否按你发现的规律变化？

规律：在平面直角坐标系中，将点(x，y)向右(或左)平移a个单位长度，可以得到对应点(x+a，y)(或(　　　 ，　　　 ))；将点(x，y)向上(或下)平移b个单位长度，可以得到对应点(x，y+b)(或(　　　 ，　　　 ))．

教师说明：对一个图形进行平移，这个图形上所有点的坐标都要发生相应的变化；反过来，从图形上的点的坐标的某种变化，我们也可以看出对这个图形进行了怎样的平移．

例　 如图(1)，三角形ABC三个顶点坐标分别是A(4，3)，B(3，1)，C(1，2)．

(1)将三角形ABC三个顶点的横坐标后减去6，纵坐标不变，分别得到点A₁、B₁、C₁，依次连接A₁、B₁、C₁各点，所得三角形A₁B₁C₁与三角形ABC的大小、形状和位置上有什么关系？

(2)将三角形ABC三个顶点的纵坐标都减去5，横坐标不变，分别得到点A₂、B₂、C₂，依次连接A₂、B₂、C₂各点，所得三角形A₂B₂C₂与三角形ABC的大小、形状和位置上有什么关系？

引导学生动手操作，按要求画出图形后，解答此例题．

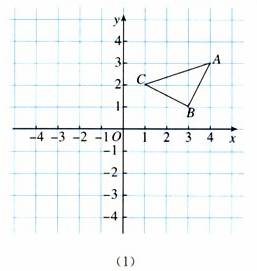
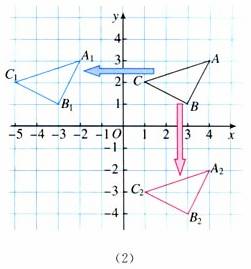
解：如图(2)，所得三角形A₁B₁C₁与三角形ABC的大小、形状完全相同，三角形A₁B₁C₁可以看作将三角形ABC向左平移6个单位长度得到．类似地，三角形A₂B₂C₂与三角形ABC的大小、形状完全相同，它可以看作将三角形ABC向下平移5个单位长度得到．

思考题：

由学生动手画图并解答．

归纳：

上节课我们学习了用坐标表示地理位置，本节课我们继续研究坐标方法的另一个应用．

教材第59页第3题．