
根据学生已有的认知基础及本课教材地位和作用,特从四个方面对教学目标分析。
1、知识技能:使学生掌握在平面直角坐标系中点或图形的平移引起的点的坐标变化规律。
2、教学重点与难点。
通过分析,我们看到“用坐标表示平移”在教材中起到承上启下的作用,有着广泛的应用,因此本节课的重点是在直角坐标系中,探究点或图形的平移引起的点的坐标变化规律。
对应点的坐标变化规律的获得过程,教科书中仅用了两个栏目,很少的篇幅,对于这些规律,不是要学生死记硬背,而是要学生具备一定的探究归纳能力,对七年级的学生来说,有较大的难度,因此本课的难点是在坐标系中结合图形的平移变换理解和应用对应点的坐标变化规律。
6.2.2《用坐标表示平移》教案
教学任务分析
|
教 学 目 标 |
知识技能 |
使学生掌握平面直角坐标系中的点或图形平移引起的点的坐标的变化规律 |
|
数学思考 |
使学生看到平面直角坐标系是数与形之间的桥梁,感受到代数与几何的相互转化,初步建立空间观念,发展几何直觉 |
|
|
解决问题 |
通过探究归纳出点或图形的平移引起的点的坐标的变化规律,积累数学活动经验,提高学生科学思维素养 |
|
|
情感态度 |
体验数学活动充满探索性与创造性,激发学生学习数学的兴趣,使学生经历数学思维过程获得成功体验 |
|
|
重点 |
在平面直角坐标系中,探究点或图标的平移引起的点的坐标变化规律 |
|
|
难点 |
在坐标系中结合图形平移变换理解对应点的坐标的变化规律和解决有关问题 |
教学流程安排
|
活动流程图 |
活动内容和目的 |
|
活动1 创景引趣 活动2 探究归纳 活动3 培养创新 活动4 反馈练习 活动5 实际运用 活动6 小结巩固 |
激发学生的学习兴趣,认识到生活中蕴含的大量数学信息 探究点的左右上下平移引起点的坐标变化规律 探究线段的平移引起端点的坐标变化规律,初步具备数学创新的能力和动手操作、自主探索、合作交流的学习方式 明白研究对三角形、实物的平移引起对应点坐标变化规律可归结为研究图形顶点情况。 将实际问题抽象成数学模型,用点的平移与坐标的变化规律解决简单实际问题,积累数学活动经验 强化学生对知识理解和记忆,提高分析和小结能力。 |
教学过程设计
|
问题与情境 |
师生行为 |
设计意图 |
|
「活动1」 观看短片 思考有哪些画面在作平移变换 |
教师播放短片 教师提出问题 学生思考、联想、发表见解 在活动1中,教师应关注: ⑴学生能否观察、发现 ⑵学生能否参与认识和联想 |
通过给学生提供现实背景及生活素材,吸引学生的注意力,创设良好学习氛围 激发好奇心和求知欲,激发爱国热情,并认识到现实生活中蕴含着大量的数学信息 |
|
问题与情境 |
师生行为 |
设计意图 |
|
「活动2」 如图1写出点A坐标( )   图1 图1⑴把点A向右平移5个单位长度,坐标变为A1( ) 再把点A向上平移4个单位长度,坐标变为A2( ) 观察坐标变化,你能从中发现什么规律?如果把点A向左或向下平移,猜想规律又会是什么?试试看。 ⑵把点A向左平移5个单位长度,坐标变为A3( ) 再把点A向下平移4个单位长度,坐标变为A4( ) 观察坐标变化,你又能从中发现什么规律? ⑶综合⑴⑵你能用你自己的语言归纳你发现的规律吗? ⑷自己再找几个点,对它们进行平移,观察它们的坐标是否按你发现的规律变化。 |
学生观察、思考、探究,小组交流,发表个人见解 教师课件显示,提出问题 在本次活动中,教师应关注: ⑴学生能否通过坐标的变化,发现横、纵坐标中谁变谁没变; ⑵能否发现前横坐标、左右平移单位长度、新横坐标三者之间的关系; ⑶能否发现前纵坐标,上下平移的单位长度、新纵坐标 |
⑴让学生经历一个由特殊到一般的归纳过程,让学生有足够的时间,使学生充分活动起来,通过探究并发现规律。 ⑵体现知识的发生、形成、发展过程,体会到探究--发现--归纳--验证的学习的方式和数形结合的思想。 |
|
「活动3」 如图2所示,已知平面直角坐标系中一条线段AB,A、B两点坐标分别为(3,4)、(0,0)   图2 图2⑴把线段AB向右或向左平移__个单位,坐标变为(____,____),重复操作并作好记录,你能发现什么规律?填在横线上____ ⑵把线段AB向上或向下平移__个单位,坐标变为(____,____)重复操作并作好记录,你能发现什么规律,填在横线上____ |
学生动手操作,作好记录,小组合作交流 教师用课件展示,并参与引导鼓励每个同学尽可能独立思考,去获得自己的“发现 |
⑴使学生进一步经历观察、实验、探究、验证、交流、反思等活动。尝试从不同角度寻求解决问题的方法,增强学习数学的自信心; ⑵显现数学永远充满神奇的魅力,探究富有艰辛的挑战; ⑶如果说前面的活动是帮扶,则本次活动实为放,放飞学生的想象翅膀放开学生的手脚大胆创新 |
|
问题与情境 |
师生行为 |
设计意图 |
|
「活动4」 问题1 如图3所示写出 A点坐标( )B点坐标( )O点坐标( ) 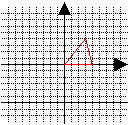  图3 图3⑴在图3中,将ΔAOB沿X轴向左平移3个单位长度,如图4所示,则A’点坐标( ),B’点坐标( )O’点坐标( ) ⑵在图3中将△AOB沿Y轴向下 平移2个单位长度,如图5所示,则 A’点坐标( ),B’点坐标( ) O’ 点坐标( ) 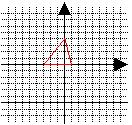    图4 图5 |
教师课件展示 学生注意图形每平移一次引起坐标的变化情况 本次活动中教师应关注: ⑴对于图形的平移引起图形顶点坐标的变化; ⑵对应点的坐标发生了怎样的变化 |
⑴通过填空练习,学生可进一步了解点的坐标与图形的平移之间的关系; ⑵让学生明白研究图形的平移引起的对应点的坐标的变化规律可归结为研究图形顶点的情况 ⑶本题意在综合考查点的坐标、图形平移后的坐标变化及动手操作、绘图能力 |
问题2 如图6  图6 图6⑴请你写出A、B、C、D、E、F、G的坐标; ⑵源源想把A船上平移7个单位长度,再 向右平移8个单位长度,你能帮他办到吗? 请作出相应图案,并写出平移后的7个点 的坐标 |
|
问题与情境 |
师生行为 |
设计意图 |
|
「活动5」 老师事先把宝藏藏在某个同学的座位里,现提供一张“探宝路线图”,图7中每个方格代表一个座位,出发点是王莉同学座位。 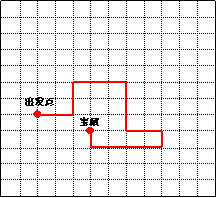  图7 图7(1)你知道宝藏在哪个同学的位置上吗? (2)建立适当的直角坐标系,如果出发点坐标为(0,2),试用坐标写出要走的线路和宝藏位置。 |
学生参加游戏活动 教师课件展示转化 教师主要关注: ⑴学生能否正确写出几个重要点的坐标。 ⑵提醒学生注意各点的变化情况 |
⑴让学生亲身经历将实际问题抽象成数学模型并进行包括解释与应用的过程 ⑵让学生在游戏中感受学习数学的乐趣,增长知识,体验数学服务于生活 ⑶让学生学会用点的坐标变化规律解决简单的实际问题, 让学生充分感受平面直角坐标系在解决实际问题中的作用 ⑷将枯燥的数学问题赋于有趣的实际背景,使,内容更符合学生的特点,激发学生学习数学的兴趣 |
|
「活动6」 你能谈谈你的收获吗? 布置作业: 必做题:第58页习题6.2第1、2、3、4题 选做题:第61页习题6.2第9题 |
在教师引导下学生自主归纳完成 教师明确如下: 在平面直角坐标系中 ⑴将点(x,y)向右(或向左)平移a个单位长度,纵坐标不变,可以得到对应点(x+a,y)或(x-a,y) ⑵将点(x,y)向上(或向下)平移个a个单位长度,横 坐标不变,可以得到对应点(x,y+a)或(x,y-a) 学生独立完成作业,教师批改总结 本次活动中,教师关注: ⑴不同层次的学生对知识的理解程度,有针对性的讲解 ⑵学生在练习中暴露出的问题,要及时反馈 |
给学生一个充分从事数学活动的机会,也体现了学生是数学学习的主人理念 |
教材第59页第3题.
教材第58页练习;习题6.2中第1、2、4题.
展示问题:教材第56页图.
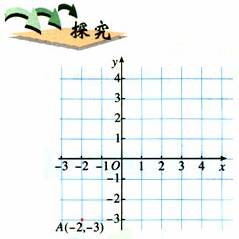
(1)如图将点A(-2,-3)向右平移5个单位长度,得到点A1,在图上标出它的坐标,把点A向上平移4个单位长度呢?
(2)把点A向左或向下平移4个单位长度,观察他们的变化,你能从中发现什么规律吗?
(3)再找几个点,对他们进行平移,观察他们的坐标是否按你发现的规律变化?
规律:在平面直角坐标系中,将点(x,y)向右(或左)平移a个单位长度,可以得到对应点(x+a,y)(或( , ));将点(x,y)向上(或下)平移b个单位长度,可以得到对应点(x,y+b)(或( , )).
教师说明:对一个图形进行平移,这个图形上所有点的坐标都要发生相应的变化;反过来,从图形上的点的坐标的某种变化,我们也可以看出对这个图形进行了怎样的平移.
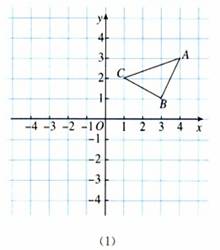
例 如图(1),三角形ABC三个顶点坐标分别是A(4,3),B(3,1),C(1,2).
(1)将三角形ABC三个顶点的横坐标后减去6,纵坐标不变,分别得到点A1、B1、C1,依次连接A1、B1、C1各点,所得三角形A1B1C1与三角形ABC的大小、形状和位置上有什么关系?
(2)将三角形ABC三个顶点的纵坐标都减去5,横坐标不变,分别得到点A2、B2、C2,依次连接A2、B2、C2各点,所得三角形A2B2C2与三角形ABC的大小、形状和位置上有什么关系?
引导学生动手操作,按要求画出图形后,解答此例题.
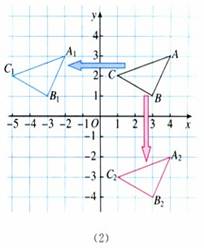
解:如图(2),所得三角形A1B1C1与三角形ABC的大小、形状完全相同,三角形A1B1C1可以看作将三角形ABC向左平移6个单位长度得到.类似地,三角形A2B2C2与三角形ABC的大小、形状完全相同,它可以看作将三角形ABC向下平移5个单位长度得到.
思考题:

由学生动手画图并解答.
归纳:

上节课我们学习了用坐标表示地理位置,本节课我们继续研究坐标方法的另一个应用.
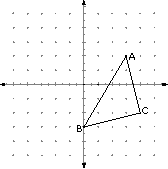
1、练习(1)
如图,△AOB沿x轴向右平移3个单位后,写出新三角形的三个顶点的坐标。
(2)如图:△AOB关于x轴的对称图形△A1OB,则对应顶点的坐标有什么变化?
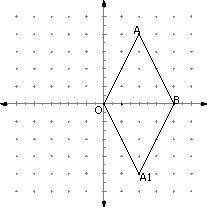 (3)沿y轴方向平移2个单位
(3)沿y轴方向平移2个单位
2、归纳:
在直角坐标系中,将点(x,y)向右(或向左)平移a个单位长度,可以得到对应点(x+a,y)[或(x-a,y)],将点(x,y)向上(或向下)平移b个单位长度,可以得到对应点(x,y+b)[或(x,y-b)]。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com