
2.(2004年扬州)龟兔赛跑,它们从同一地点同时出发,不久兔子就把乌龟远远地甩在后面,于是兔子便得意洋洋地躺在一棵大树下睡起觉来.乌龟一直在坚持不懈、持之以恒地向终点跑着,兔子一觉醒来,看见乌龟快接近终点了,这才慌忙追赶上去,但最终输给了乌龟.下列图象中能大致反映龟兔行走的路程S随时间t变化情况的是( ).

n 学法指导
² 引领激活
很多同学都看过这部影片,那么你知道“泰坦尼克”遭遇不幸时是如何向救援人员报告他们所处的具体位置?你知道最好的和最常用的方法是什么?
² 范例点评
[例1][淄博市2004年改编]根据指令[s,A](s≥0, 0°≤A<360°)机器人在平面上能完成如下动作:先在原地顺时针旋转角度A,再朝其面对的方向沿直线行走距离s. 现在机器人在平面直角坐标系的原点,且面对y轴的负方向,为使其移动到点(-3,0),应下的指令是 .
分析:解决此题首先要建立平面直角坐标系,观察点(-3,0)可知机器人向左平移3个单位,先顺时针转动900,于是应下指令为[3,900]
解: [3,900]
[例2 ][2004年深圳市南山区]
如图,是深圳市南山区地图的一角,用刻度尺、量角器测量可知,深圳大学(文)大约在南山区政府(★)的什么方向上( ).
A、南偏东80° B、南偏东10° C、北偏西80° D、北偏西10°
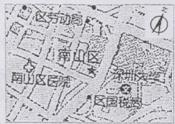
解:选A
评析:此题主要是考查同学们某一地点所处的位置.
n 师生互动
² 课堂交流
活动
选取学校门卫室所在位置为原点,分别以正东,正北方向为x轴和y轴建立平面直角坐标系,并取1cm相当于500m的比例尺,近似地作出你们小组成员的家的位置,小组内交流.
n 检测评估
1. (2004年吉林省)右图是护士统计一位病人的体温变化图,这位
病人中午12时的体温约为
( )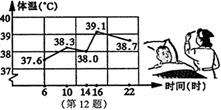 .
.
A.39.0℃ B.38.5℃
C.38.2℃ D.37.8℃
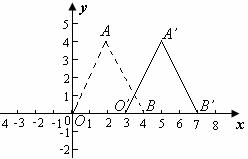
2. 如图,三角形AOB沿x轴向右平移3个单位长度之后,得到三角形 .
.
⑴三角形AOB三个顶点的坐标是A________,O_______,B_________.
⑵三角形 三个顶点的坐标是A‘_________ ,O’_______,B’_______.
三个顶点的坐标是A‘_________ ,O’_______,B’_______.
⑶沿x轴向右平移之后,三个顶点的纵坐标都___________,而横坐标都_________.
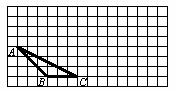
1. ⑴请在图所示的方格纸中,将三角形ABC向上平移3格,再向右平移6格,得三角形
⑵请在方格纸的适当位置画上坐标轴(1个小正方形的边长为1个单位长度),在你所建立的直角坐标系中,点C的坐标是_________.
2. 已知线段AB的两个端点 ,
,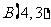 ,将线段AB向左平移2个单位长度后点A、B的坐标分别变为_________、____.
,将线段AB向左平移2个单位长度后点A、B的坐标分别变为_________、____.
活动3 探究2 坐标变化,图形是如何平移的
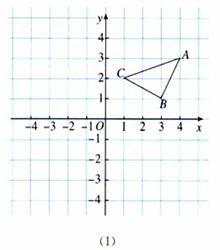
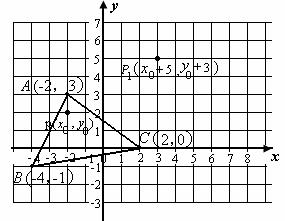
如图(1),三角形ABC三个顶点坐标分别是A(4,3),B(3,1),C(1,2).
(1)将三角形ABC三个顶点的横坐标都减去6,纵坐标不变,分别得到点A1、B1、C1,依次连接A1、B1、C1各点,所得三角形A1B1C1与三角形ABC的大小、形状和位置上有什么关系?
(2)将三角形ABC三个顶点的纵坐标都减去5,横坐标不变,分别得到点A2、B2、C2,依次连接A2、B2、C2各点,所得三角形A2B2C2与三角形ABC的大小、形状和位置上有什么关系?
思考
⑴如果将这个问题中的“横坐标都减去6”“纵坐标都减去5”相应地变为“横坐标都加3”“纵坐标都加2”,分别能得出什么结论?画出得到的图形.
⑵如果将三角形ABC三个顶点的横坐标都减去6,同时纵坐标都减去5,能得到什么结论?画出得到的图形.
通过探究2,我们发现了规律:
规律2 在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向___(或向____)平移___个单位长度;如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向___(或向 __) 平移___个单位长度.
活动4 巩固练习
如图,三角形ABC中任意一点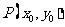 经平移后对应点为
经平移后对应点为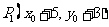 ,将三角形ABC作同样的平移得到三角形
,将三角形ABC作同样的平移得到三角形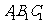 .画出三角形
.画出三角形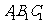 ,并写出三个顶点
,并写出三个顶点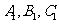 的坐标.
的坐标.
活动5 课堂小结
通过这节课的学习,你有什么收获?
课堂练习
1. 已知点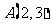 ,将点A向右平移2个单位长度后得点
,将点A向右平移2个单位长度后得点 (____,___),再将
(____,___),再将 向下平移3个单位长度后得点
向下平移3个单位长度后得点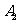 (____,____).
(____,____).
2. 培养探究的兴趣和归纳概括的能力,发展学生的形象思维能力,和数形结合的意识.
重点
掌握坐标变化与图形平移的关系.
活动1 探究1 图形平移,坐标是如何变化的
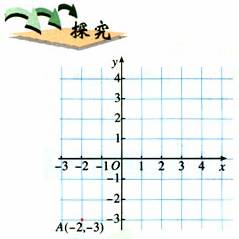 如图,⑴将点
如图,⑴将点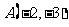 向右平移5个单位长度,得到点
向右平移5个单位长度,得到点 ,在图上标出这个点,并写出它的坐标;观察点A,A1的坐标,你能从中发现什么规律吗?⑵将点
,在图上标出这个点,并写出它的坐标;观察点A,A1的坐标,你能从中发现什么规律吗?⑵将点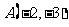 向上平移4个单位长度,得到点
向上平移4个单位长度,得到点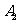 ,在图上标出这个点,并写出它的坐标;观察点A,A2的坐标,你能从中发现什么规律吗?
,在图上标出这个点,并写出它的坐标;观察点A,A2的坐标,你能从中发现什么规律吗?
再找几个点试试,观察它们的坐标是否按你发现的规律变化.
规律1 在平面直角坐标系中,将点(x,y)向右(或左)平移a(a是正数)个单位长度,可以得到对应点(x+a,y)(或( , ));将点(x,y)向上(或下)平移b(b是正数)个单位长度,可以得到对应点(x,y+b)(或( , )).
说明:对一个图形进行平移,这个图形上所有点的坐标都要发生相应的变化;反过来,从图形上的点的坐标的某种变化,我们也可以看出对这个图形进行了怎样的平移.
活动2 规律1的简单应用
1.掌握坐标变化与图形平移的关系;能利用点的平移规律将平面图形进行平移;会根据图形上点的坐标的变化,来判定图形的移动过程.
6.2.2用坐标表示平移 学案
学习目标
4.初步感受极坐标的思想.
[对话探索设计]
[探索1]
有一道题目是:
利用下面的信息,确定适当的比例尺,画出凤城三中相关地点的位置:
(1)国旗杆在校门口正东100米处;
(2)教学楼在国旗杆正东150米处;
(3)实验楼在教学楼正南300处;
(4)从国旗杆先向东走100米,再向北走100米就到图书馆.
 林奇同学根据题意画出了以下图形(小方格的边长表示实际距离50米):
林奇同学根据题意画出了以下图形(小方格的边长表示实际距离50米):
(1)他画的对不对?
(2)建立适当的平面直角坐标系,写出相关地点的坐标(规定图中1个单位长度表示实际距离1米).
 [探索2]
[探索2]
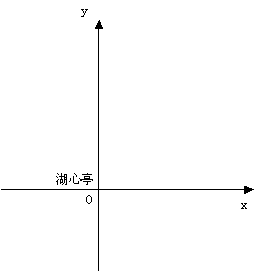
如图,以公园的湖心亭为原点,分别以正东、正北方向为x轴、y轴正方向建立平面直角坐标系,如果取比例尺为1∶10 000,而且取实际长度100米作为图中的1个单位长度,解答下面的问题:
(1)如果湖心亭在西门的正东方向200米处,请在图中描出西门的位置,并写出它的坐标;
(2)从湖心亭向东走100米,再向北走200米就到游乐场,请在图中描出游乐场的位置,并写出它的坐标;
(3)若博览会的坐标是(3,3),描出它的位置,说明它在湖心亭的什么方向上,与湖心亭的距离大约是多少(精确到米).
(4)若牡丹园的位置是在湖心亭的南偏东70º的方向上,你能确定牡丹园的位置吗?如果同时知道牡丹园在博览会的正南方向呢?如果能够,写出它的坐标(精确到0.1).
 [探索3]
[探索3]
我们知道,平面直角坐标系是由两条互相垂直、原点重合的数轴组成,习惯上把x轴画成水平的,并取向右为正方向.如图,如果已知点A的坐标为(5,0),你能画出坐标系吗?如果同时知道点B的坐标为(20,0)呢?
[探索4]
 如图,如果点A的横坐标是3,你能求出它的纵坐标吗?你能由此求出点B的坐标吗?
如图,如果点A的横坐标是3,你能求出它的纵坐标吗?你能由此求出点B的坐标吗?
 [探索5]
[探索5]
如图,如果取比例尺为1∶500 000,你能用两种不同的思路描述点B相对于点O的位置吗?点B的坐标是否被唯一确定?为什么?
[探索6]
如图,如果在某个平面直角坐标系中A、B两点的坐标分别是(3,1)和(8,1),你能由此画出这个坐标系吗?

[作业]
P60.习题5(规定:座号为单号的同学取实际距离100米为坐标系中的1个单位长度, 座号为双号的同学取实际距离1米为坐标系中的1个单位长度.), P60.习题8, P61.10
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com