练习册

  • 练习册
  • 试题
     0  205499  205507  205513  205517  205523  205525  205529  205535  205537  205543  205549  205553  205555  205559  205565  205567  205573  205577  205579  205583  205585  205589  205591  205593  205594  205595  205597  205598  205599  205601  205603  205607  205609  205613  205615  205619  205625  205627  205633  205637  205639  205643  205649  205655  205657  205663  205667  205669  205675  205679  205685  205693  447090 

    2、了解角平分线，并能够画出一个角的平分线；

    试题详情

    1、在用量角器和直尺画一个角等于已知角的基础上，能够用圆规和直尺画一个角等于已知角；

    试题详情

    教师活动
    		 学生活动
    		 点评
    一、创设情境，引入课题
    师：同学们日常生活中有许多与角有关的实物图形，先看多媒体(多媒体引入一些生活中常见的角如：羚羊的角，钟的时针与分针所成的角，家具的角，五角星等)下面请你们展示角的实物图形.
    		 学生们各自拿出角的图形如：剪刀、小闹钟、三角板、圆规等.还有形体动作“V”.
    		 引入课题，引导学生举出生活中有关角的实例，特别是形体动作“V”(太精彩了)对同学们的回答予以表扬，同学们热情高涨，纷纷举手回答.
    　　 师：同学们喜欢看足球比赛吗？球星们的每一次射门都会赢来观众阵阵喝彩，你知道射门也有技巧吗？(多媒体显示)图中的点A，B，C表示足球比赛中3个不同的射门位置.
    　　　　　

    　

    　　　 A

    　　　　　　　 　　　　　　　　　　　C

    　　　　　　　　　 B

    (1)　　　 先估测图中所示各个角的大小，再用量角器量一量比较它们的大小.

    (2)　　　 与同学交流度量角的方法.

    如果射门角度越大，则进球机会越大.请指出图中哪一点射门最好.

    		 学生各自拿出量角器，在书上测量并相互交流度量角的方法，课堂气氛活跃.
    　
    　
    生：在课本上量出
    ∠A=300∠B=870
    ∠C=460。
    在B处射门最好。
    		 激发学生的学习热情，吸引学生的注意力。
    引导学生回顾量角器的使用方法，学生讨论归纳，“一对中，二合线，三读数”的操作要领。对学生的回答给予掌声鼓励。
    二、探索活动
    活动一：
    师：回顾小学里学过的角的概念：
    		 学生小组交流，课堂气氛活跃。
    		 同学们积极动脑筋，尤其能说出角的两种定义，真不简单。
    教师活动
    		 学生活动
    		 点评
    　　 角是由两条具有公共端点的射线组成的。两条射线的公共端点是这个角的顶点。这两条射线是这个角的边。
    　　 角也可以看成是一条射线绕着它的端点旋转而形成的。
    　师：强调(1)每个角都有两条边，这两条边都是射线。
    　　　　 (2)角的两边有公共端点-顶点
    (3)顶点两边是构成角的两个要素。
    师：提问：角是如何表示的，同学们交流一下。
    拿出四张准备好的卡片让四位学生表示：
    ①　　　　 角可以用一个数字来表示,一般地,用一个数字表示一个角时,需在角内靠近顶点处画上弧线.∠1
    ②　　　　 用三个字母表示时,表示顶点的字母必须写在另两个字母的中间.∠AOB
    ③　　　　 角可以用希腊字母α来表示.∠α
    ④　　　　 角还可以用它的顶点字母来表示.如右图.∠A
    　
    		 　
    　
    　
    学生小组讨论激烈，使课堂气氛达到高潮，最后归纳出四种表示方法。
    　
    　　 1　　　　 ∠1
    　　　　　 B
    　　　　　　 C
    　　　　　　 ∠AOB
    O　　　　　 A

    　

    　　　 α　　　 ∠α

    　

    　　　　　　　 ∠A

    　A

    四位同学在以上卡片上表示。

    		 课堂气氛活跃,由小学知识归纳出角的四种表示法,并为以后的书写规范打下伏笔.
    　
    　
    　
    　
    　
    　
    　
    　
    　
    　
    　
    老师对四位同学的表示给予评价。
    活动二:
    试一试:问题1
    如图打台球时,球的反射角总等于入射角.请估测图中入射角的度数,估测反弹后会撞击图中哪一点?

    　

    　　　　　　　　　　　 O

    　　　　　　　　　　　　　　　　　 D

    　

    　　　　　　　　　　　　　　　　　 C

    　

    　　　　　　　　 F　　　　　　　 A　 B

    用量角器量出图中所示角的度数,检验你的估测.

    		 打台球是同学们喜欢的游戏.在活动中,用量角器测量出入射角等于反射角.
    生:小球反射时必过A 点.
    生:角的大小:
    ∠FOA＜∠FOB＜∠FOC＜∠FOD
    用叠合的方法可得出上述结论.
    		 在这样的活动中男同学们显得很活跃,因为他们玩过打台球,所以很快就能说出答案.
    问题2.(1)如图以OA为一边的角有哪几个?请按大小顺序用“＜”号连接这些角.
    (2)如图中∠AOC=∠AOB+∠BOC
    　　　　 ∠AOB=∠AOD-∠DOB
    类似地你还能写出哪些有关角的和与差的关系式?请与同学交流.
    　　　　　　　　　 D
    　　　 O
    　　　　　　 　　　C
    　
    　 A　　　 B
    　
    　
    		 生:(1)图中以OA为一边的角有∠AOB,∠AOC,∠AOD,由图知∠AOB＜∠AOC＜∠AOD
    (2)由图知
    ∠AOB=∠AOC-∠BOC
    ∠BOC=∠AOC-∠AOB
    ∠AOD=∠AOB+∠BOD=∠AOB+∠BOC+∠COD∠BOD=∠BOC+∠COD等等
    		 给学生充分的独立思考相互交流的时间和空间，鼓励学生尽可能多地表述出有关角的和与差的关系式。充分发挥学生学习的积极性，体现了教学过程中学生的主体地位。
    教师活动
    		 学生活动
    		 点评
    试一试：
    (多媒体演示，学生拿出地理书P48页中国地图)　 三架飞机从广州O出发分别飞往昆明A、北京B、上海C、连结OA、OB、OC以OB为边有哪些角？量出这些角的度数并写出这些角的和与差的关系式？　 B
    　　　　　　　　　　　　　
    　
    　　　　　　 A　　　　　　　　 C
    　
    　
    　　　　　　　　　　　 O
    		 学生动手在地图上连结，用量角器很快找到答案。
    生：以OB为边的角有∠AOB=830
    ∠BOC=32.50
    和差关系：∠AOC=∠BOC+∠AOB，∠AOB=∠AOC-∠BOC，∠BOC=∠AOC-∠AOB。
    		 联系实际，既培养了学生动手操作的实践能力，又培养了学生的学习兴趣。突破本节课的难点。
    三，练一练：
    　关于角的度量单位，，我们常用度、分、秒、来表示。10=60′,1′=60〞与时间进制类似。
    (1)　　　 把18015′化为用度表示的角。
    (2)　　　 把93.20化为用度、分、秒表示的角。
    (3)　　　 学生操练课本P206/1、2
    		 独立完成，两位同学到黑板上计算，并作讲解，巩固度、分、秒之间的换算关系。
    生1：解：(1)先把
    15′化成度，即
    15′=(15/60)0=0.250所以
    18015′=18.250
    生2：解：因为
    10=60′，所以0.20=60’×0.2=12′，因此93.20=93012′。
    		 注意作业的书写格式，其他同学做在作业本上，教师行间巡视并作评价，对两位同学的讲解表示肯定，掌声鼓励，激发学生的学习兴趣，抓住本节课的重点。
    四，思考题：
    还记得成语“四面八方”吗？八个方向是不够用的，方位角是我们日常生活中经常碰到的问题，如北偏东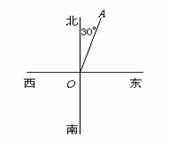
    　
    300等，下面的问题请同学们思考：(多媒体显示)
    　　 如图A、B、C三点分别代表动物园，游乐场，肯德基餐厅中的某一处，动物园和游乐场分别在肯德基餐厅的北偏西方向，动物园又在游乐场的北偏东方向，那么图中对应的点A应是 　　　，点B应是　　　 　，点C应是　　　　　　 ，
    		 　
    　
    　
    　
    　
    　
    　
    　
    　
    　
    　
    　
    　
    　
    同学们大组讨论，非常激烈，又一次把课堂气氛推向高潮。
    生：集体回答：A是动物园，B是游乐场，C是肯德基餐厅。
    		 　
    　
    　
    　
    　
    　
    从日常生活中所遇到的问题出发，以本节课的知识为载体，建立数学模型，再利用数学模型去解决实际问题，体现了数学来源于实践，反过来又应用于实践的辨证唯物主义观点。
    教师活动
    		 学生活动
    		 点评
    　　　　　　　　　　 A
    　　　　　　　　　　　 动物园
    　　　　 B
    　
    　　　 游乐场

    　

    　　　　　　　　　　　　　　 C

    　　　　　　　　　　 肯德基餐厅

    		 　
    		 　
    五，交流总结：
    (1)　　　 认识并会表示角，知道角的度量单位度，分，秒，会进行简单的换算.
    (2)　　　 会比较、估计角的大小，能根据图形写出图中有关角的和与差的关系式，能联系实际识别角及方向.
    		 学生小组讨论交流，两个学生代表总结本节课的内容，其他同学补充，培养学生的文字口头表达能力.
    		 本节课让学生在主动参与，自主探索，合作学习的过程中，通过动手、动脑，学会观察、发现、分析、概括.培养学生解决实际问题的能力.
    六，布置作业：P209/ 1，2，3

    试题详情

    　　　　　　　　　　 学生：和角有关的实物，量角器，中国地图.

    试题详情

    　　 教学难点：　　　 根据图形写出图中有关角的和与差的关系式.

    试题详情

    2.联系生活实践，感受用角去确定方位.

    　　 情感与态度目标；在数学学习活动中获得成功的体验.

    试题详情

    知识技能目标：1.了解角的相关概念，掌握角的表示方法.

    2.能估计一个角的大小，会使用量角器量角的大小，认识度、分、秒，会进行简单换算，能写出角的和与差的关系式.

    　　 过程性目标：　 1.通过学生动手画角、量角等实践活动，体验角的特征和角的大小的意义.

    试题详情

    6.略

    试题详情

    6．2.1　 用坐标表示地理位置

    温故知新　　 由(1)和(2)总结出：一般地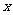轴上点的坐标表示为P(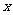，0)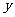，轴上点的坐标表示为P(0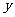，)，(3)，(4)省略。

    引领激活　 由学生熟悉的地理知识，最好的和最常用的方法－－－－－报告经纬度(34oW，45oN)，救援人员就根据(34oW，45oN)这一对实数找到了出事的位置，抽象得出用一对实数来表示平面内点的位置的数学问题。

    课堂交流　 略，小组内交流

    检测评估　　　 1.C　 2.B　 3.O2,(6,-1)　 4.略　 5.A(-3,1);B(-2,-1);C(1,-1);D(3,0)

    试题详情

    6.有一个运算装置，当输入值为x时，其输出值为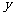，且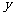与x之间存在某种对应关系，已知输入值为,0,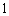时, 相应的输出值分别为5,,．

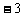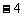    你能把这些有序数对在平面直角坐标系上描出吗?

    试题详情


    同步练习册答案