6.2　 中位数与众数

(第二课时)

[教学目标]

4．小结

　　 (1)一般地，设有n个数据，首先将这n个数据由小到大(或由大到小)依次排列．

　　 若n是奇数，则把最中间位置的一个数据称为这组数据的中位数；若n是偶数，则把最中间位置的两个数据的平均数称为这组数据的中位数．

　　 (2)一般地，在一组数据中，我们把重复出现次数最多的那个数据称为这组数据的众数．

3．例题教学　　

　　 教师根据实际情况，考虑是否安排例题．

2．探索活动

　　 通过探索活动，让学生认识到此时平均数和中位数并没有什么意义，从而引进众数．一般来说，商店应多进众数所对应的尺码的男衬衫．为了便于学生理解众数的概念，可考虑补充一些应用众数的实例．

1．情境创设

　　 (1)课本提供的情境，是为了说明“平均数”不能准确反映“平均水平”，教学中也可设计其他的情境，只要一组数据中，个别数据与其他数据有很大的差异即可．

(2)结合课本中的“讨论”，还可选用以下的情境：一家鞋店在一段时间内销售了某种女鞋111双，其中各种尺码的鞋销售量如下：

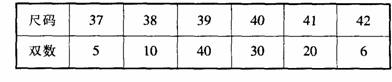
　　 这些数据的平均数约等于39.6码，中位数等于 39.5码．事实上，根本就不存在39.6码和39.5码的鞋子，此时平均数和中位数并没有什么意义．在这个问题中，鞋店比较关心什么?

3．能对日常生活中的有关问题与现象做出一定的评判．

[教学过程]

2．能结合具体的情境理解平均数、中位数和众数的区别与联系，并能根据具体问题，选择合适的统计量表示数据的集中程度．

1．掌握中位数、众数等数据代表的概念，能根据所给的信息求出一组数据的中位数、众数．

6.2　 中位数与众数

(第一课时)

[教学目标]

4．小结

　　 平均数、中位数和众数从不同角度描述了一组数据的集中程度，刻画了一组数据的“平均水平”．其中，又以平均数的应用最为广泛．它们都有一定的优缺点．

　　 中位数是通过排序得到的，它不受最大、最小两个极端数值的影响；而平均数是通过计算得到的，因此它会因每一个数据的变化而变化．例如，在体操比赛中，为了避免个别裁判不正常打分的影响，一般是先去掉一个最高分和-个最低分，然后求余下分数的平均数，这样就能减少极端数据对一组数据的“平均水平”的影响．中位数在一定程度上综合了平均数和中位数的优点，具有比较好的代表性．

　　 众数也是数据的一种代表数，反映了一组数据的集中程度．例如，我们用众数的方法，能够统计出一般人所穿衬衫或裤子最受欢迎的尺寸．日常生活中诸如“最佳”、“最受欢迎”、“最满意”等，都与众数有关系，它反映了人们的一种最普遍的倾向．

　　 平均数、中位数和众数它们都有各自的的优缺点．

　　 平均数

　　 (1)需要全组所有数据来计算；

　　 (2)易受数据中极端数值的影响．

　　 中位数

　　 (1)仅需把数据按从小到大的顺序排列后即可确定；

　　 (2)不易受数据中极端数值的影响．

　　 众数

　　 (1)通过计数得到；

　　 (2)不易受数据中极端数值的影响．