3．每组至少完成100次实验，分别记录下其中相交和不相交的次数．

2．取一张白纸，在上面画一组平行线．它们之间的距离为2厘米，另外准备一根1厘米长的针．在纸下面垫一层柔软的东西，使针落在纸面上时不会弹跳起来．

6．由折线统计图，估计钉帽着地的概率．

　　 (注意：①图钉必须从一定高度自由落下，保证着地时的随机性；②组内同学合作时要进行适当的分工；③体现学生的自主性，实验活动以及实验数据的汇总等都可以由学生白行组织完成；④教师认真评价学生合作交流的意识和能力，学生的思维水平，学生的动手能力等)

　　 [师生共析]我们一同来研究一下，掷一枚图钉时，出现“钉帽着地”这一结果的概率．

　　 将图钉掷200次，每掷20次，统计一下两个组同学“钉帽着地”这一结果出现的次数，并算出相应的频率，如下表．

将统计数据(“钉帽着地”的频率)画成折线统计图，看起来更直观．

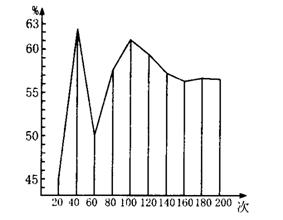
从图中可发现，“顶帽着地”的频率开始“摆动”得很厉害，随着试验次数的增加，这个

频率就开始比较稳定了，最后大致在56.5%左右摆动．由此我们可以估计“顶帽着地”的概率约为56．5%，即0.565.

　　 [师]在数学的历史上，有一个较为著名的投针实验：

　　 平面上画着一些平行线，相邻的两条平行线之间的距离为a，向此平面任投一长度为l(l<a)的针，该针可能与其中某一条平行线相交，也可能与它们都不相交．

　　 相交和不相交的可能性相同吗?你能通过列表或画树状图求出该针与平行线相交的概率吗?

　　 [生]相交和不相交的可能性不相同，由于结果的可能性不同，因此这个事件的概率也不能列表或画树状图求出该针与平行线相交的概率．也必须用“当实验次数较大时，实验频率稳定于理论概率”来估计该针与平行线相交的概率．

　　 [师]很好，我们还是分组活动．

　　 活动二：平面上画着一些平行线，相邻的两条平行线之间的距离都是a，向此平面任投一长度为l(l<a)的针，该针可能与其中某一条平行线相交，也可能与它们不相交，估计针与平行线相交的概率．

　 　活动目的：利用“当实验次数较大时，实验频率稳定于理论概率”，并据此估计针与平行线相交的概率．

　　 活动方式：小组交流，全班研讨的方法．

　　 活动工具：每组学生要在平面上画有相同距离“的一组平行线，并且有长度都为l的针(l<a)．要求针必须粗细均匀．

　　 活动步骤：1．分组，两人一组．

5．汇总全班各小组其一个组．两个组、三个组、四个组……的实验数据，相应得到实验100次、200次、300次、400次……时钉帽着地的频率，并绘制折线统计图．

4．分别汇总本小组其中两人、三人、四人、五人的实验数据，相应得到实验40次、60

次、80次、100次时钉帽着地的频率，填写下表，并绘制折线统计图．

3．根据上表你认为哪种情况的频率较大?

2．每组每人做20次实验，根据实验结果，

填写下表的表格：

2．亲历实验，提高学生学习数学的兴趣．

教学重点

　　 能用实验的方法估计一些复杂的随机事件发生的概率．

教学难点

　　 借助大量重复实验去感悟实验频率稳定于理论概率．

教学方法

　　 小组活动．

教具准备

　　 大头针，图钉，多媒体演示

教学过程

　　 Ⅰ．提出质疑，引入新课

　　 [师]上节课我们介绍了用树状图或列表格的方法计算随机事件的概率．也就是计算一些事件的概率就可以在某个试验之前，算出某个结果的概率．但这些方法有一个前提条件，是什么?

　　 [生]要求实验出现的各种结果是等可能的，并且实验出现的结果必须是有限个．

　　 [师]下面我们来看一个例子．比如掷一枚图钉，有几种结果?它们是等可能的吗?

　　 [生]有“朝天”和“倾斜”两个可能结果，但我觉得这两个可能的结果不是等可能的.

　　 [师]能不能说“朝天”的概率是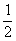，“倾斜”的概率也是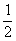呢?

　　 [生]当然不能．

　　 [师]再例如，掷一只墨水笔尖，也有“正”“反”两种可能，但出现的可能性相等吗?

　　 [生]不相等．

　　 [师]很好．一个试验，虽然结果有有限个，但各个结果出现的可能性不相等，这时怎样求某一事件的概率呢?

　　 [生]只有动手做大量的试验．因为我们知道：当实验次数很大时，实验频率稳定于理论概率，并可据此估计某一事件发生的概率．

　　 [师]看来，求这些事件发生的概率只有亲自做很多次实验了．

　　 Ⅱ．讲授新课

　　 活动一：从一定高度落下的图钉，落地后可能钉尖着地，也可能钉帽着地．你估计哪种事件发生的概率大?

　　 活动目的：利用“当实验次数较大时，实验频率稳定于理论概率”来估计某一事件发生的概率．

　　 活动方式：小组合作交流，全班汇总实验数据，交流研讨．

　　 活动工具：形状、大小完全相同的图钉．

　　 活动步骤：1．分组：每组5人．

1．激发学生实事求是的科学态度．