
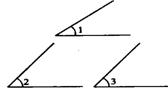
 解:
解:  与
与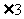 相等.
相等.

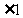 与
与 互余,
互余, 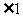 与
与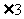 互余.
互余.
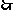
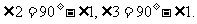 (余角的定义)
(余角的定义)
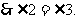 (等量代换)
(等量代换)
想一想:如果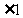 与
与 互补,
互补, 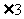 与
与 互余,
互余,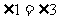 ,那么
,那么 与
与 有怎样的关系?为什么?(引导学生模仿例题的说理过程,说明
有怎样的关系?为什么?(引导学生模仿例题的说理过程,说明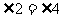 的过程及理由.)
的过程及理由.)
2. 互为余角、互为补角的性质.
同角(或等角)的余角相等. 同角(或等角)的补角相等.
2.已知3组角:

(1) 对A组中的每一个角,在B组中找出它的补角,并用线连接;
(2) B组中有哪些角的余角在C组中?分别找出这些角, 并用线连接.
1.填表

想一想,同一个角的补角与它的余角之间有怎样的数量关系?
2.做一做.
1. 互为余角、互为补角的概念.
如果两个角的和是一个直角,这两个角叫做互为余角.简称互余.其中一个角叫做另一个角的余角.
如果两个角的和是一个平角,这两个角叫做互为补角.简称互补.其中一个角叫做另一个角的补角.
注:⑴角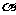 的余角表示为
的余角表示为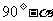 ,角
,角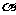 的补角表示为
的补角表示为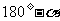 .
.
⑵互余、互补是指两角在数量(度数)上存在着一种特殊关系.与位置无关.
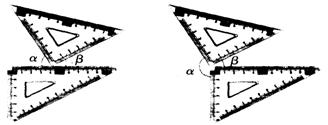
通过直观、形象的演示,引导学生观察,引入余角、补角的概念.
10、如图,直线AB、EF相交于点D,∠ADC=90 º E
(1)∠1的对顶角是_____________; 1 2
∠2的余角有__________________ A B
(2)若∠1与∠2的度数之比为1:4,求∠CDF、∠EDB的度数. F
9、直线AB、CD相交于点O,OE是∠AOD的平分线,∠FOC=90 º,∠1=40 º,求∠2与
∠3的度数.
E
 D
D
A 2 B
3 1
 C
C
C
C
F
8、 如图,直线AB、CD相交于O,已知∠AOC=70 º,OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3,求EOD的度数.
如图,直线AB、CD相交于O,已知∠AOC=70 º,OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3,求EOD的度数.
A D
O E
C B
6、 直线AB、CD相交于O,且∠AOC+ 7、如图,直线AB、CD相交于点O,OE平分∠BOD,
 ∠BOD=120 º,求∠AOC的度数.
∠DOE=30 º,求∠AOC的度数. B E D
∠BOD=120 º,求∠AOC的度数.
∠DOE=30 º,求∠AOC的度数. B E D
 C
B
C
B
O O
A D
C A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com