3.　理解一元二次方程的根就是二次函数与x轴交点的横坐标.

2.　理解二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系，理解何时函数有两个交点、一个交点和没有没有交点.

1.　经历探索二次函数与一元二次方程的关系的过程，体会方程与函数之间的关系.

2．你能利用a、b、c之间的某种关系判断二次函数y=ax²+bx+c的图象与x轴何时有两个交点、一个交点，何时没有交点？

1．求下列二次函数的图象与x轴交点坐标，并作草图验证．

(1)y=x²－2x；(2)y=x²－2x－3．

[例1]已知二次函数y=kx²－7x－7的图象与x轴有两个交点，则k的取值范围为 ．

[例2]抛物线y=ax²+bx+c与x轴交于点A(－3，0)，对称轴为x=－1，顶点C到x轴的距离为2，求此抛物线表达式．

[例5]有一个二次函数的图象，三位学生分别说出了它的一些特点：

甲：对称轴是直线x=4；

乙：与x轴两个交点的横坐标都是整数；

丙：与y轴交点的纵坐标也是整数，且以这三点为顶点的三角形面积为3．

请写出满足上述全部特点的一个二次函数表达式　　　　　　　　　　　 ．

在同一坐标系中画出二次函数y=x²+2x,y=x²-2x+1,y=x²-2x+2的图象并回答下列问题：

(1)每个图象与x轴有几个交点？

(2)一元二次方程? x²+2x=0,x²-2x+1=0有几个根?验证一下一元二次方程x²-2x+2=0有根吗?

(3)二次函数y=ax²+bx+c的图象和x轴交点的坐标与一元二次方程ax²+bx+c=0的根有什么关系?

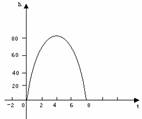
我们已经知道,竖直上抛物体的高度h(m)与运动时间t(s)的关系可用公式h=-5t²+v₀t+h₀表示,其中h₀(m)是抛出时的高度,v₀(m/s)是抛出时的速度.一个小球从地面以40m/s的速度竖直向上抛出起,小球的高度h(m)与运动时间t(s)的关系如图所示,那么

(1)h和t的关系式是什么？

(2)小球经过多少秒后落地?你有几种求解方法?与同伴进行交流.

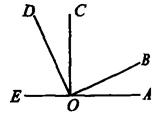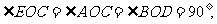5.　　　 如图,问图中有与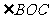互补的角吗?

[小结]　 这节课你学到了什么?

[课后作业]

　　　　　 《补充习题》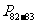　 余角、补角、对顶角(1)

　　　　 《随堂练123》 余角、补角、对顶角(1)

4.　　　 一个角的补角加上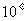,等于这个角的余角的3倍,求这个角.