
3.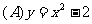 下列函数的图象中,与x轴没有公共点的是( )
下列函数的图象中,与x轴没有公共点的是( )
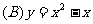
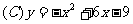
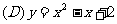
2.方程 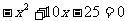 的根是
;则函数
的根是
;则函数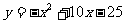 的图象与x轴的交点有 个,其坐标是
.
的图象与x轴的交点有 个,其坐标是
.
1.方程 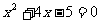 的根是
;则函数
的根是
;则函数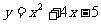 的图象与x轴的交点有 个,其坐标是
.
的图象与x轴的交点有 个,其坐标是
.
不画图象,你能判断函数 的图象与x轴是否有公共点吗?请说明理由.
2.根据一元二次方程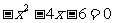 根的情况,判断二次函数
根的情况,判断二次函数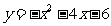 的图象与x轴交点坐标是什么?
的图象与x轴交点坐标是什么?
(讨论、归纳)一元二次方程与二次函数的关系.
根据一元二次方程的根的情况,可以知道二次函数的图象与x轴的位置关系.
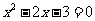
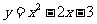 (探究) 1.观察二次函数 的图象,你能确定一元二次方程
根吗?
(探究) 1.观察二次函数 的图象,你能确定一元二次方程
根吗?
2.观察下列图象,分别说出一元二次方程x2-6x+9=0和x2-2x+3=0的根的情况.
(讨论、归纳)二次函数与一元二次方程的关系.
(探究) 1.根据一元二次方程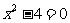 根的情况,判断二次函数
根的情况,判断二次函数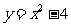 的图象与x轴交点坐标是什么?
的图象与x轴交点坐标是什么?
打高尔夫球时,球的飞行路线可以看成是一条抛物线,如果不考虑空气的阻力,球的飞行高度y(单位:米)与飞行距离x(单位:百米)满足二次函数 :y= -5x^2+20x(显示出图象)问:这个球飞行的水平距离最远是多少米?
(由讨论引出课题)
(1)y=x2+4x-5;(2)y=-x2+6x-9;(3)y=2x2+3x+5
反馈练习2:判断下列二次函数图象与x轴的交点情况
(1) y=x2-1;(2)y=-2x2+3x-9;(3)y=x2-4x+4;
(4)y=-ax2+(a+b)x-b(a、b为常数,a≠0)
反馈练习3:二次函数y=x2-2x-3和一次函数y=x+b有唯一公共点(即相切),求出b的值.
∵y=x2-2x-3=( )2_______ ∴图象的顶点为( )
列表
|
x |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
…… |
|
y |
|
|
|
|
|
|
|
…… |
描点、连线
(1)一次函数y=x+2的图象与x轴的交点为( , )
一元一次方程x+2=0的根为________
(2) 一次函数y=-3x+6的图象与x轴的交点为( , )
一元一次方程-3x+6=0的根为________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com