
P11页1、2、3
同学们,这节课我们学会了什么?
从上面的例子中,我们看到这样的一对角,它们的顶点重合,它们的两条边互为反向延长线。我们把这样的2个角叫做互为对顶角。其中一个角叫做另一个角的对顶角。
如图,有几对对顶角。
探索:如图,直线AB与CD相交于点O,则∠AOC与∠BOD的大小关系是什么?
对顶角的性质:对顶角相等。
 如图,直线AB、CD相交于点O,OE平分∠AOC,∠AOE=250。你能说出图中哪些角的度数?请与同学交流。
如图,直线AB、CD相交于点O,OE平分∠AOC,∠AOE=250。你能说出图中哪些角的度数?请与同学交流。


例题:如图,AB、CD相交于点O,∠DOE=900,∠AOC=720。求∠BOE的度数。
例、已知直线AB、CD、EF相交于O点,OG是∠AOF的平分线,∠BOD=320,∠COE=240,求∠AOG的度数。
(一)、 情境引入
情境引入

 1、如何,测量古塔的底座的角度。
1、如何,测量古塔的底座的角度。

2、 小孔成像:我国古代的墨子对光学很有研究,它发现光是直线传播的。利用这个原理,他让一个人站在屋外,在阳光的照射下,它在窗户上钻一个小孔,这时,在屋内的墙上出现一个倒立的人像。这就是后来的摄影技术的先声。
小孔成像:我国古代的墨子对光学很有研究,它发现光是直线传播的。利用这个原理,他让一个人站在屋外,在阳光的照射下,它在窗户上钻一个小孔,这时,在屋内的墙上出现一个倒立的人像。这就是后来的摄影技术的先声。
2、概念及性质的运用
1、对顶角的概念和性质。
目的与要求 了解对顶角的概念,熟练掌握对顶角的性质。
知识与技能 能准确地画出图形,掌握角的关系的应用。
情感、态度与价值观 树立严谨科学的学习态度,培养说理论证能力,会进行图形语言和符号语言的相互转化。
探究一:(1)观察图象,x为何值时,y=0?
(2)此时函数图象与x轴的交点与一元二次方程根的关系?
一般地,如果二次函数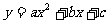 的图象与x轴有两个公共点(
的图象与x轴有两个公共点(  ,0)、(
,0)、( 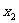 ,0 ),那么一元二次方程
,0 ),那么一元二次方程 有两个不相等的实数根
有两个不相等的实数根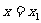 、
、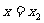 ,反之亦成立.
,反之亦成立.
巩固练习----相信自己,享受学习成果
探究二:(1)观察二次函数 的图象(图1)和二次函数
的图象(图1)和二次函数 的图象(图2),分别说出一元二次方程
的图象(图2),分别说出一元二次方程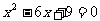 和
和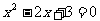 的根的情况.
的根的情况.


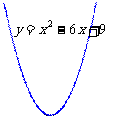
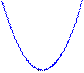

图1 图2
(2)二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?
|
二次函数y=ax2+bx+c的图象和x轴交点 |
一元二次方程ax2+bx+c=0的根 |
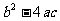 |
|
有两个交点 |
有两个不相等的实数根 |
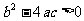 |
|
有一个交点 |
有两个相等的实数根 |
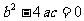 |
|
没有交点 |
没有实数根 |
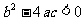 |
巩固练习----相信自己,享受学习成果
写出二次函数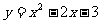 的顶点坐标、对称轴,并画出它的图象.
的顶点坐标、对称轴,并画出它的图象.
二次函数的一般形式是什么?与什么有点像?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com