
3.关注学生能否用计算器产生的随机数进行模拟实验.
2.鼓励学生思维的多样化.
4.每按一次 键,计算器就产生一个1-12之间的整数,并显示在显示器的第二行.
键,计算器就产生一个1-12之间的整数,并显示在显示器的第二行.
(不同的计算器产生随机数的方法可能不同,教学时,可引导学生利用自己所使用的计算器探索产生随机数的具体步骤)
我们用计算器能产生一个1-12之间的一个随机整数,我们如何用计算器模拟刚才的实验呢?
[做一做]两人组成一个小组,利用计算器产生1-12之间的随机数,并记录下来,每产生6个随机数为一次实验,每组做10次实验,看看有几次实验中存在2个相同的整数.将全班的数据集中起来,估计6个1-12之间的整数中有2个数相同的概率.
(要求学生利用计算器实际进行模拟实验,如果学生的计算器不具有产生随机数的功能,那么可以引导学生用其他方法进行模拟实验,如有放回的抽签等.当然,实验结果未必有很好的精确度,只要让学生体会到实验次数很大时结果将较为精确即可.这里的结果未必和上一课时的估计结果一致,但要让学生体会到两者的差异只是由实验次数的差异造成的,当实验次数很大时,两者应较为相近)
[评价指导]1.主要评价学生的参与程度、活动过程中的思维方式,与同学合作交流的情况.
3.按键 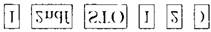 ,输入所产生的随机数的范围.
,输入所产生的随机数的范围.
2.按 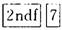 键,利用
键,利用 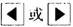 或
或  键选择RANDI,并按
键选择RANDI,并按 键,进入产生随机数的状态.
键,进入产生随机数的状态.
1.打开计算器.
3.在数学活动中获得成功的体验,锻炼克服困难的意志,建立自信心.
教学重点:利用计算机或计算器等进行模拟实验。估计一些复杂的随机事件发生的概率.
教学难点:用模拟实验代替实际凋查,估计一些随机事件的概率.
教学方法:探索交流法.
教具准备:①多媒体课件;②计算器.
教学过程
Ⅰ.创设问题情境,引入新课
[师]我们上节课利用全班的调查数据设计了不同方案。估计6个人中有2个人生肖相同的概率.要想使这种估计尽可能精确,就要尽可能多地增加调查对象,而这样做既费人力又费物力.能不能不用调查即可估计出这一概率呢?请同学们在小组内交流,思考具体方案.
Ⅱ.讲授新课
[生]不同的生肖有12个,而我们要估计的是6个人中有2个人生肖相同的概率.可以设计一个自由转动的转盘,并将其等分成面积相等的十二个扇形.分别在每个扇形区域标出相应的生肖或绘出相应的生肖图,然后自由转动转盘6次,记下每次转出的生肖,为一次实验.重复多次实验,即可估计出6个人中有2个人生日相同的概率。
[生]也可以取扑克牌中任何一种花色12张分别代表12个生肖.这样每个人的生肖都对应着一张扑克牌.6个人中有两个人生肖相同.就意味着6张扑克牌中有2张扑克牌完全相同.因此,我们充分“洗”过这12张扑克牌后,从中抽取一张,记下它的牌面数字,放回去;再重新“洗”牌,从中抽取一张,记下它的牌面数字,放回去……直至重新“洗”牌后.从中抽取一张,记下第6个牌面数字。为一次实验.重复多次实验,即可估计6个人中有2个人生肖相同的概率.
[生]还可以用12个编有号码的,大小相同的球代替12种不同的生肖.这样每个人的生肖都对应着一个球.6个人中有2个人生肖相同,就意味着6个球中有2个球的号码相同.因此,可在口袋中放入这样的12个球,从中摸出1个球,记下它的号码,放回去;再从中摸出1个球,记下它的号码.放回去……直至摸出第6个球,记下第6个号码,为一次实验.重复多次实验,即可估计6个人中有2个人生日相同的概率.
[师]同学们设计的方案都是合理的,都应给予肯定和鼓励.但为什么每次摸出球后都要放回去呢?
[生]为了保证每次摸球时,12个球被摸到的可能性是相同的.保持实验的随机性. [师]上面的方法是用摸球实验代替实际调查,类似这样的实验移为模拟实验.
[议一议]除了用大小相同的12个球进行模拟实验外,你还能想出其他方法吗?
[师]事实上,还可以利用计算器产生的随机数进行模拟实验.
使用计算器产生随机数的大体步骤是:进入产生随机数的状态,输入所产生的随机数的范围,按键得出随机数.具体来说计算器产生随机数的过程如下:
2.形成实事求是的态度以及进行质疑和独立思考的习惯.
1.鼓励学生积极参与数学活动,培养学习数学的兴趣.
2.鼓励学生的思维多样化,避免思维的单一性.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com