
6.3 用计算器求平均数
[教学目标]
4.练习:用计算器模拟上节课的生日问题.
备课资料
消息的传播
大家都知道,消息的传播是很快的,那往往是这样假定的:一传十,十传百,百传千……
现在,假定在某-个有200人的小村庄里,开始有一个人向三个人传出某种消息,第二天,听到消息的三个人中,有-个人把消息传了开去.不过,他也只传了三个人。第三天,刚听到消息的三个人中,也只有一个人把消息传开去,而且也只传三个人……
在这样的假定下,传播的速度似乎并不十分快.因为不是一传三,三传九,九传二十七……而是每天只传三个,半个月最多不过传了45人,不到全村人数的四分之一。
但是,有一个出乎意料的情况,半个月之后,几乎必定有人重复听到这一消息.
根据计算.经过15次传播之后,至少有1个人重复听到消息的概率达到99.45%。
你信不信?如果有疑问,可以设计一则实验来验证这个结论.
准备200张卡片,在上面分别写上1,2,3,…,200,将卡片装入布袋里.
第一次从布袋中盲目地取出一张,把号码记下,这个号码就算是消息的发布者,暂时不放回。
第二次,从布袋中盲目取出三张,记下号码,这算是第一批听到消息的三个人,留一张
暂时不放回(这张卡片代表下一次传播消息的人),另两张放回。
把第一张卡片放回,然后第三次从布袋中盲目取三张卡片,记下号码.这算是第二批听到消息的三个人.留一张暂时不放回,其余两张放回.
把第二次摸出的并暂时留下的一张卡片收回,然后第四次从布袋中摸……
看一下,15次后,有没有被重复摸出的?
上述消息传播问题是很有实用价值的,比如,在医疗事业中,必须十分注意疾病的重复感染问题,因为传染病的传播就像消息传播一样,既然重复听到消息的可能性是很大的,当然重复感染的可能性也是很大的。
3.做一做:合作交流用计算器产生随机数进行模拟实验.
2.议一议:计算器产生随机数的过程.
1.用模拟实验估计6个人中有2个人生肖相同的概率:
方案-:制作卡片、抽签.
方案二:自山转动的转盘.
方案三:利用,计算器产生随机数,进行模拟实验.
2.用计算器模拟实验,估计生活中一些复杂的随机事件发生的概率.你还能设计出不同的模拟实验方案吗?
Ⅵ.活动与探究
某种“15选5”的彩票的获奖号码是从1-15这15个数字小选择5个数字(可以重复),若彩民所选择的5个数字恰与获奖号码相同,即可获得特等奖.小明观察了最近100期获奖号码,发现其中竟有51期有重号(同一期获奖号码有2个或2个以上的数字相同),66期有连号(同一期获奖号码中有2个或2个以上的数字相邻).他认为获奖号码不应该有这么多重号和连号,获奖号码可能不是随机产生的,有失公允.小明的观点有道理吗?重号的概率大约是多少?利用计算器模拟实验可以估计重号的概率.
[过程]两人组成一个小组,利用计算器产生1-15之间的随机数.并记录下来,每产生5个随机数为一次实验,每组做10次实验,看看有几次重号和连号.将全班的数据汇总集中起来,就可估计出1-15之间的整数中随机抽出5个数出现重号和连号的概率.
出现重号的概率等.
[结果]小明的观点没有道理。实际上,在完全随机的情况下,出现重号和连号的概率比较大.例如:出现重号的理论概率是1-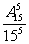 ≈0.53.当然学生只能通过模拟实验宋体会这一点. 板书设计
≈0.53.当然学生只能通过模拟实验宋体会这一点. 板书设计
§ 6.3.2 生日相同的概率(二)
1.习题6.5第2题.
3.如果手头没有硬币,那么你能用什么办法模拟掷硬币的实验?你能用计算器模拟该实验吗?做一做,看看结果如何?
解:用计算器进行模拟实验,如可将产生的随机数1对应硬币的正面,而将随机数2对应硬币的反面.如果计算器只有产生,0-1之间随机小数的功能,那么可将0-0.5之间的随机数对应硬币的正面,而将0.5-1之间的随机数对应硬币的反面.可以两人组成一个小组,每组做这样的模拟实验50次,看出现0-0.5之间的数有几个,出现0.5-1之间的数有几个,将全班的数据集中起来,就可估计出硬币投出后,正面(或反面)朝上的概率.
Ⅳ.课时小结
生活中.为了尽可能使实验所得频率稳定于理论概率,并且用频率去估计理论概率,使这种估计尽可能精确,就需要尽可能多地增加调查对象,而这样做即费时又费力,于是为了节省时间和精力,用模拟实验代替实际调查,用计算器产生的随机数进行模拟实验.经历实验、统计等活动过程,在活动中进一步发展了学生合作交流的意识和能力,提高了思维水平.
Ⅴ.课后作业
2.老师有5张电影票,现在要将他们随机分给班上的5个同学,为了保证公正,你能利用计算器帮老师作出决定吗?
解:如班级有45人,可以利用计算器产生5个1-45之间的随机整数,学号与这5个随机数相同的同学将获得电影票,当然,这5个数中可能有重复的.此时,可以利用计算器再产生几个随机数,只要最终产生5个不同的数即可.
1.用计算器模拟实验估计50个人中有2个人生日相同的概率:
两人组成一个小组。利用计算器产生1-366之间的随机数,并记录下来,每产生50个随机数为一次实验,每组做5次实验,看看有几次实验中存在2个相同的整数.将全班的数据集中起来,估计50个1-366之间的整数中有2个数相同的概率.
(利用计算器模拟实验解决上一课时的生日问题,以加强前后知识的联系,这里的结果未必与上一课时的估计一致,但要让学生进一步体会到两者的差异只是由实验次数的差异造成的,当实验次数很大时,两者应是较为相近的.同时,让学生真正地体会到模型实验既不费时也不费力是一个很好的用实验、统计估计概率的方法)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com