
2.掷一枚骰子一次得到2点的概率是_________;
1.从一幅52张扑克牌中任抽一张得到Q的概率为_________;
6.某公司生产的A种产品,它的成本是2元,售价是3元,年销售量为10万件.为了获得更好的效益,公司准备拿出一定的资金做广告.根据经验,每年投入的广告费是x(10万元)时,产品的年销售量将是原销售量的y倍,且y是x的二次函数,它们的关系如下表:
|
x(10万元) |
0 |
1 |
2 |
… |
|
y |
1 |
1.5 |
1.8 |
… |
(1)求y与x的函数表达式;
(2)如果把利润看作是销售总额减去成本和广告费,试写出年利润S(10万元)与广告费x(10万元)函数表达式;
(3)如果投入的广告费为10万元-30万元,问广告费在什么范围内,公司获得的年利润随广告费的增大而增大?
5.有一种螃蟹,从海上捕获后不放养最多只能存活两天.如果放养在塘内,可以延长存活时间.但每天也有一定数量的蟹死去,假设放养期内蟹的个体重量基本保持不变.现有一经销商,按市场价收购了这种活蟹1000kg放养在塘内,此时市场价为30元/kg,据测算,此后1kg活蟹的市场价每天可上升1元.但是,放养一天需各种费用支出400元,且平均每天还有10kg蟹死去,假定死蟹均于当天全部售出,售价都是20元/kg.
(1)设x天后1kg活蟹的市场价为P元,写出P关于x的函数表达式;
(2)如果放养x天后将活蟹一次性出售,并记1000kg蟹的销售总额为Q元,写出Q关于x的函数表达式;
(3)该经销商将这批蟹放养多少天后出售,可获得最大利润(利润=销售总额-收购成本-费用)?最大利润是多少?
4.某医药研究所进行某一治疗病毒新药的开发,经过大量的服用试验后知,成年人按规定的剂量服用后,每毫升血液中含药量y微克(1微克=10-3毫克)随时间x小时的变化规律与某一个二次函数y=ax2+bx+c(a≠0)相吻合.并测得服用时(即时间为0时)每毫升血液中含药量为0微克;服用后2小时每毫升血液中含药量为6微克;服用后3小时,每毫升血液中含药量为7.5微克.
(1)试求出含药量y(微克)与服药时间x(小时)的函数表达式,并画出0≤x≤8内的函数图象的示意图.
(2)求服药后几小时,才能使每毫升血液中含药量最大?并求出血液中的最大含药量.
(3)结合图象说明一次服药后的有效时间是多少小时?(有效时间为血液中含药量不为0的总时间)
3.某商场销售某种品牌的纯牛奶,已知进价为每箱40元,生产厂家要求每箱售价在40元-70元之间.市场调查发现,若每箱以50元销售,平均每天可销售90箱;价格每降低1元,平均每天多销售3箱;价格每升高1元,平均每天少销售3箱.
(1)写出平均每天销售量y(箱)与每箱售价x(元)之间的函数表达式(注明范围);
(2)求出商场平均每天销售这种年奶的利润W(元)与每箱牛奶的售价x(元)之间的二次函数表达式;(每箱利润=售价-进价)
(3)求出(2)中二次函数图象的顶点坐标,并求出当x=40,70时W的值,在直角坐标系中画出函数图象的草图;
(4)由函数图象可以看出,当牛奶售价为多少时,平均每天的利润最大?最大利润是多少?
2.将进货为40元的某种商品按50元一个售出时,能卖出500个.已知这时商品每涨价一元,其销售数就要减少20个.为了获得最大利益,售价应定为多少?
1.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.
(1)若商场平均每天要盈利1200元,每件衬衫应降价多少元?
(2)每件衬衫降低多少元时,商场平均每天盈利最多?
2.某类产品按质量共分为10个档次,生产最低档次产品每件利润为8元,如果每提高一个档次每件利润增加2元.用同样的工时,最低档次产品每天可生产60件,每提高一个档次将少生产3件,求生产何种档次的产品利润最大?
1.关于二次函数y=ax2+bx+c的图象有下列命题:
①当c=0时,函数的图象经过原点;②当c>0且函数图象开口向下时,方程ax2+bx+c=0必有两个不等实根;③当a<0,函数的图象最高点的纵坐标是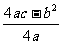 ;④当b=0时,函数的图象关于y轴对称.其中正确命题的个数有(
)
;④当b=0时,函数的图象关于y轴对称.其中正确命题的个数有(
)
A.1个 B.2个 C.3个 D.4个
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com