2.形成解决问题的一些基本策略.体验解决问题策略的多样性，发展实践能力和创新精神.

1.结合具体情境.初步感受统计推断的合理性.

4．池塘里有多少条鱼

知识与技能目标：

　　 进一步体会概率与统计之间的联系，用样本去估计总体的统计思想.

过程与方法目标：

2.进一步体会概率与统计之间的关系.

教学难点：结合具体情境，初步感受统计推断的合理性.

教学方法：活动探究法.

教具准备：多媒体演示.

教学过程

　　 Ⅰ.创设问题情境，引入新课

　　 [师]同学们都知道在《西游记》里有一个深受大家喜爱的人物，他神通广大，只要有妖魔出入的地方总有他的身影……

　　 [生]孙悟空、孙大圣……

[师]但这个无所不能的大圣今天却遇到了一个难题，听老师细细给你们讲来：

　　 话说孙悟空弃了养马的官，从天宫回到花果山之后，树起了齐天大圣的旗帜，天天练兵，准备与玉皇大帝派来的天兵天将决一死战.

　　 “立正!”大圣向小猴兵们发出号令.

　　 “嘻嘻!什么立正?”这些小猴子仍在叽叽喳喳，东蹦西跳.有话说“猴子屁股坐不住”，其实“猴子双腿也立不正”.

　　 “重来一遍，立正--报数！”

　　 “嘻嘻!报什么数?”

　　 大圣面对着这群小猴子，心中有点不快，训练了几天，立正，稍息，报数，样样都不成.

　　 “连究竟有多少猴兵也弄不清，这可怎么办呢?”大圣束手无策了.

　　 “这好办，”大圣的参谋长在一旁说.

　　 “你有什么好的主意？”

　　 “立正，报数这一套在花果山上行不通，大圣，您干脆把这些猴兵放了吧！”

　　 “集合起来，还东溜西窜的，放了还数得清数目?”

　　 “放假三天，一定能数清.”

　　 “你别说胡话了!”大圣不悦地说.

　　 参谋长在大圣耳边轻轻说了一番，喜得大圣拍手叫好.

　　 “参谋长，真有你的!”

　　 原来参谋长有他的妙计.

　　 第二天，大圣和参谋长，在小猴兵中随意拉了100只猴子，将这些猴子头上的毛剃去一片，然后叫他们归队.

　　 大圣向众小猴宣布：“这些日子来，训练很有成绩，因此本大圣决定放假三天.”

　　 大圣的话音未落，小猴兵们早已跑得无影无踪了.

　　 你知道孙大圣的参谋长想出了怎样的妙计吗?

　　 其实在我们生活中也遇到过和孙大圣同样的问题.例如：要想知道鱼缸里有多少条鱼，只要数一数就可以了，但要估计一个鱼塘里有多少条鱼，该怎么办呢?

　　 通过这节课的学习，相信大家一定会有切实可行的办法.

　　 Ⅱ.讲授新课

　　 [师]我们先考虑一个比较简单的问题--摸球问题(多媒体演示).一个口袋中有8个黑球和若干个白球，如果不许将球倒出来数，那么你能估计出其中的白球数吗?

　　 请同学们对此问题展开讨论，获得一定的方案.

　　 [生]根据我们学过的求概率的方法.如果一个袋子里有2个白球，3个黑球，任意摸出一个球是黑球的概率有两种求法.一种是理论概率的求法，因为任意摸出一个球有5种等可能的结果，而摸出的是黑球有3种等可能的结果，所以任意摸出一球是黑球的概率为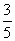；一种是用实验的方法，任摸出一个球叫做一次实验，当实验次数很大时，实验频率稳定于理论概率，据此来估计任意摸出一球是黑球的概率.因此一口袋中有8个黑球和若干个白球，设白球有x个，则从袋中摸出一球是黑球的概率为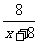；然后我们通过多次实验，我们又可以估计出从口袋中随机摸出一球是黑球的概率，利用它和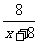约相等，即可估计出自然数x.

　　 [生]也可以用抽样调查的方法，从口袋中随着摸出10个球，求出其中黑球数与10的比，再把球放回口袋中，不断重复上述过程.通过这样多次抽样调查，求出样本中的黑球数与10的比值的“平均水平”，这个“平均水平”根据抽样的随机性应近似于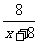，据此也可以估计出x的值.

　　 [师]通过我们这两位同学解释，初步感受到统计推断的合理性，体会了统计与概率之间的关系.

　　 下面是小明和小亮的做法，是不是和你们想法有点不谋而合的感觉.

　　 多媒体演示：

小明是这要做的：从口袋中随机摸出-球，记下其颜色.再把它放回口袋中，不断重复上述的过程，我们共摸了200次，其中有57次摸到黑球，因此我估计口袋中大约有20个白球.

　　 你能说说他这样做的道理吗?

　　 小亮是这样做的：利用抽样调的方法。从口袋中一次摸出10个球.求出其中黑球数与10的比值，再把球放回口袋中.不断重复上述过程.我总共摸了20次，黑球数与10的比值的平均数为0.25，因此，我估计口袋中大约有24个白球.

　　 你能说说他这样做的道理吗?

　　 [生]我认为小明这样做的道理是：假设口袋中有x个白球，通过多次实验，我们可以估计出从口袋小随机摸出一球，它为黑球的概率57／200；另一方面，这个概率又等于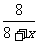，据此可得

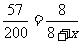　　 解得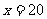

　　 所以由此可估计出白球数约有20个

　　 [生]小亮这样做的道理是：同样设口袋里有x个白球，通过多次抽样调查，求出样本中黑球数与总球数比值的“平均水平”，这个“平均水平”应近似于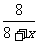.由于小亮求出的平均水平为0.25，据此可得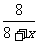＝0.25.

　　 解，得x＝24，所以可估计出白球数有24个.

　 　[师]这种估计比较粗略，但我们知道这些常用的估计方法在现实生活中应用比较广泛.

　　 下面我们通过具体的实践活动，切实感受小明和小亮做法的合理性.

　　 多媒体演示：

做一做

分组进行下面的活动：

在每个小组的口袋中放入已知个数的黑球和若干个白球.

(1)分别利用上述两种方法估计口袋中所放的白球数.

(2)打开口袋，数数口袋中白球的个数，你们的估计值和实际情况一致吗?为什么?

(3)全班交流，看看各组的估计结果是否一致，各组结果与实际的情况差别有多大?

(4)将各组的数据汇总，并根据这个数据估计一个口袋小的白球数，看看估计结果又如何?

(5)为了使估计结果较为准确，应该注意些什么?

　　 (在具体操作中，学生的实验结果与实验数据应该存在偏差，这很正常，个别小组的结果可能差异较大，但学生通过各组数据的汇总而得到的估计值应该和实际情况差别较小，具体操作时，若没有白球、黑球，也可用大小相近的不同颜色的豆子代替)

　　 [师]你们小组的估计值和实际情况一致吗?

　　 [生]估计值和实际情况有偏差.

　　 [师]为什么会有这种偏差呢?

　　 [生]因为我们用实验估计的概率和理论概率有偏差.

　　 [师]很好，所以小明和小亮的方法可能还比较粗略，如果将各组的数据汇总，并根据这个数据估计一个口袋中的白球数，看看估计结果如何?

　　 [生]汇总后得到的估计值和实际情况差别较小.

　　 [师]为了使估计结果较为准确，应该注意什么?

　　 [生]摸球要保证随机性，摸球时，要充分把袋子中的球搅匀.

　　 [生]实验次数越多越准确.

　　 [师]那么通过亲自实践，我们除感受到上述两种方法合理外，还存在着估计的偏差，但它们在现实生活中意义却很重要，请同学们思考：它们各有哪些优缺点?

　　 [生]从理论上讲，如果实验次数足够多，那么小明的方法应当比较准确，但这种方法的现实意义不大，相比较而言，小亮的方法具有现实意义，当然，当总数较小时，用小亮的方法估计，其精确度较差，但对许多实际问题(其总数往往较大)，这种精确度是允许的，而且这种方法方便可行.

　　 (在比较这两种方法时，学生的看法可能多种多样，只要他们的想法有一定道理，教师就应予以肯定和鼓励)

　　 多媒体演示：

想一想

如果口袋中只有若干个白球，没有其他颜色的球，而且不许将球倒出来数，那么你如何估计出其中的白球数呢?与同伴交流.

　　 [生]可以向口袋中另放几个黑球，也可以从口袋中抽出几个球并将它们染成黑色或作上标记.

　　 [师]还记得我们最开始讲的故事《孙大圣点兵》吗?孙大圣的参谋长到底想出什么办法?你会接着把这个故事讲完吗?

　　 [生]第三天，大圣和参谋长派了担任警卫的士兵到前山后山上去捕捉小猴兵，一会儿，捕来了200只，大圣上前一检查，发现其中4只是“头上无毛”的.

　　 “200只中，有4只是头上无毛的，说明在山里随意抓1只猴子，恰巧抓到‘头上无

毛’的频率是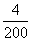，即，也可以说，概率大约是.”

　　 “而现在一共有100只猴子是‘头上无毛’的，所以，所有猴子大约有5000只.”

　　 “我手下有雄兵半万！”大圣哈哈大笑：“参谋长你这个办法真妙!”

　　 不过，这里要提醒同学们注意，“头上无毛”的猴子虽和其他猴子混合在一起，但毕竟不是绝对均匀分布在山里的，所以，随意捕200只猴子，“头上无毛”的不一定总是4只.如果“头上无毛”的是5只，3只，那么随之估计的猴兵总数也就不是5000个了.这种方法仅仅是个估计，这个估计可能会与事实有出入，而且有时还可能有很大的出入.这说明，用局部调查得到的资料来估计整体的情况，有可能会作出错误的判断，但是，只要有相当数量的调查数据，调查方法又是正确的，“估计数与事实有较大出入”的可能性(也就是概率)是很小的，所以，这种估计还是很有价值的.

　　 [师]你还能设计一个方案估计鱼塘中鱼的总数吗？

　　 [生]可以像孙大圣的参谋长一样，先从池塘里捞出若干条鱼，将它们作上标记，然后再放回鱼塘，经过一段时间后，再从中随机捕捞若干条鱼，并以其中有标记的鱼的比例作整个鱼塘中有标记的鱼的比例，据此可估计鱼塘中鱼的数量.

　　 [师]真棒!利用这种方法还可以解决生活中的哪些问题?清举例说明.

　　 [生]生物工作者为了研究某个地区的生态状况，往往需要估计这一地方各种生物的数量，例如濒临灭绝的一种鸟的数量.可以先捕获一定数量的鸟，给它们作上标记放回森林，经过一段时间后，再从中随机捕获若干只这样的鸟，并以其中有标记的鸟的比例作为种群中有标记的鸟的比例，据此就可估计森林小所有这种鸟的数量.

　　 [师]真精彩，你将来-定是一个保护环境的科学工作者，祝贺你.

　　 Ⅲ.课时小结

　　 本节课我们经历了具体的情境，如孙大圣点兵，估计池塘里的鱼等，初步感受统计推断的合理性，进一步体会了概率和统计之间的联系，小明和小亮的估计方法，特别是小亮的估计方法在现实生活中具有很重大的意义，例如在生物学的研究中，生物学家经常要估计某个种群的数量等.

　　 Ⅳ.课后作业

　　 习题6.6第1题.

　　 Ⅴ.活动与探究

　　 赤峰某地区为估计该地区黄羊的只数，先捕捉20只黄羊给它们分别作上标记，然后放还，待有标记的黄羊完全混合于黄羊群后，第二次捕捉40只黄羊，发现其中两只有标记，从而估计这个地区有黄羊__________只.

　　 (2003午内蒙古赤峰)

　　 [过程]第二次捕捉40只黄羊，并以其中有标记的2只黄羊的比例作整个赤峰某地区

有标记的黄羊的比例，据此估计该地区黄羊的数量.

　　 [结果]估计这个地区有黄羊x只，则

　　 2：40＝20：x，

　　 x＝400.

　　 即该地区估计有黄羊400只.

2.初步认识数学和人类生活的密切联系及对人类历史发展的作用,体验数学活动充满着探索与创造，感受数学的应用意识.

教学重点：1.结合具体情境，初步感受统计推断的合理性.

1.积极参与数学学习活动.对数学有好奇心和求知欲.

4.初步形成评价与反思的意识.

3.学会与人合作，并能与他人交流思维过程和结果.

2.形成解决问题的一些基本策略.体验解决问题策略的多样性，发展实践能力和创新精神.

1.结合具体情境.初步感受统计推断的合理性.