
3、无论x取什么值,下列不等式都成立的是 ( )
A、 B、
B、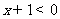 C、
C、 D、
D、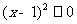
2、无论x取什么值,下列不等式都成立的是 ( )
A、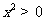 B、
B、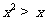 C、
C、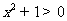 D、
D、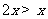
1、x与5的和的一半是非负数用不等式可以表示为 ( )
A、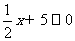 B、
B、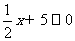 C、
C、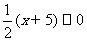 D、
D、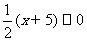
6、用不等式表示下列数量之间的关系:
(1)如图,小明与小聪玩跷跷板,大家都不用力时,跷跷板左低右高。小明的身体质量为 p(kg),小聪的身体质量为q(kg),书包的质量为2kg,怎样表示p 、q之间的关系?

(2)(如图,天平左盘放三个乒乓球,右盘放5g砝码,天平倾斜。设每个乒乓球的质量为x(g),怎样表示x与5之间的关系?

 (3)下图是公路上对汽车的限速标志,表示汽车在该路段行使的速度不得超过40km /h。若用v (km /h)表示车的速度,那么v与40之间的数量关系用怎样的式子表示?
(3)下图是公路上对汽车的限速标志,表示汽车在该路段行使的速度不得超过40km /h。若用v (km /h)表示车的速度,那么v与40之间的数量关系用怎样的式子表示?
(4)据科学家测定,太阳表面的温度不低于6000 ℃.设太阳表面的温度为t (℃),怎样表示t 与6000之间的关系?
(5)要使代数式 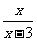 有意义,x的值与3之间有什么关系?
有意义,x的值与3之间有什么关系?
(6)某水果批发市场规定:批发苹果不少于1000千克时,可享受每千克2.2元的最优批发价,个体水果经营户小王携款x元到该批发市场除保留200元作生活费外,全部以最优惠批发价买进苹果.用不等式表示问题中x与已知数量间的不等关系。
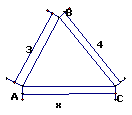
5、如图,一只蚂蚁从A地到C地,所行的路程x应满足
4、比较下列各数的大小,用“<”或“>”填空:
(1)-3______-2; (2)-1______ 0;
(3) 3______-4; (4)-5______-6;
(5)
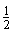 ______
______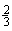 ; (6)-
; (6)-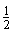 ______-
______-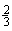 。
。
3、用不等式表示:
(1)2x与1的和小于零 ;
(2)a的2倍与4的差是正数 ;
(3)b的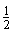 与c的和是负数
;
与c的和是负数
;
(4)x的绝对值与1的和不小于1 。
2、对于任意有理数x,下列不等式一定成立的是( )
A、2x<6 B、2x2<6 C、2x2+6>0 D、2x>6
1、在数学表达式:①-3 <0,②3x+5 > 0,③ x² - 6,④x=-2,⑤y ≠0,⑥ x+2 ≥ x中,不等式的个数是( )
A、2 B、3 C、4 D、5
3、小明今年x岁,小强今年y岁,爷爷今年m岁,小明年龄的3倍与小强年龄的6倍之和不小于爷爷年龄.
答:3x+6y≥m
[范例点睛]
例1用不等式表示下列各数或数量关系:
(1)a的3倍与b的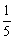 的和不大于3;
的和不大于3;
(2)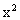 是非负数;
是非负数;
(3)x的相反数与1的差不小于2;
(4)x与17的和比它的5倍小.
思路点拨: (1)中不大于就是小于或等于,即“≤”;(2)中的非负数就是大于等于零,即“≥”;(3)不小于就是大于或等于;(4)中关键词“小”等.
易错辨析:对“非负数”、“至多”、“至少”、“不大于”等这样的表述,未能准确使用不等式的符号,如对x≥2和x>2认为是同一个不等式;
方法点评:用不等式表示数或数量关系,这与列代数式、列方程一样,都是将语言叙述的数量关系转化为数学式子。
例2用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C的含量及购买这两种原料的价格如下表:
|
原 料 维生素及价格 |
甲种原料 |
乙种原料 |
|
维生素C(单位/千克) |
600 |
100 |
|
原料价格(元/千克) |
8 |
4 |
(1)现配制这种饮料10千克,要求至少含有4200单位的维生素C,试写出所需甲种原料的质量x(千克)应满足的不等式.
(2)如果还要求购买甲、乙两种原料的费用不超过72元,那么你能写出x(千克)应满足的另一个不等式吗?
思路点拨:先弄清题意,找出不等关系。(1)至少含有4200单位的维生素C,所以600x+100(10-x)≥4200;(2) 费用不超过72元,所以8x+4(10-x)≤72.
易错辨析:(1)维生素C、原料的费用来源于甲、乙两种原料;(2) 10-x在解题中是一个整体,需加括号。
方法点评:解题时一定要搞清不等关系,以及每个数量的具体含义。
[课外链接]
数学史话:柯西不等式
柯西(Cauchy,1789-1857),法国19世纪最杰出的数学家之一。他生于巴黎,少年时就显示出数学才能,得到大数学家拉格朗日、拉普拉斯等人赏识。他27岁时成为法兰西科学院院士和工科大学教授。柯西的数学工作遍及理论数学和应用数学各个领域,写出了800多篇数学论文和三部重要数学论著。
下面介绍的柯西不等式是数学中的一个著名不等式,其应用极其广泛。
设a1,a2,a3,…,an和b1,b2,…,bn是两组实数,则有
(a1b1+a2b2+…+anbn)2≤(a12+a22+…+an2)(b12+b22+…+bn2)
其中,等号当且仅当 时成立。
时成立。
请你分别用两组具体的数代入柯西不等式,进行验证。
[随堂演练]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com