
2、经历由具体问题建立不等式的过程,初步体会不等式是刻画现实世界的一种数学模型。
1、感受生活中存在的大量不等关系,了解不等式的意义。
2、某工程队爆破石头,导火线燃烧的速度为0.8cm /s,点火工人跑开的速度是5m/s,安全区在离点火地110m外,,设这根导线的长度至少应大于xcm,点火工人才能到达安全区,列出不等式.
1、(2005,安徽中考题)根据下图,对a、b、c三种物体的重量判断正确的是( )
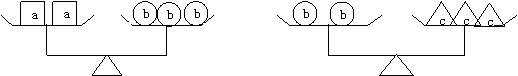
A a<c B a<b C a>c D b<c
2、 .
不等式:像30kg<55kg 、x>50,x+2<48、a≤100、3y≥10等,用不等号表示不等关系的式子叫做不等式.
尝试练习:
例1用“>”或“<”号填空:
(1)-6+4 -1+3; (2)5-2 0-2;
(3)6×2 3×2 (4)-6×(-4) -2×(-4).
练习:课本P.7习题7.1-1
说明:数的比较大小方法:正数大于负数;两个负数比较大小,绝对值大的负数反而小.
例2用不等式表示:
(1)a是正数; (2)b是非负数; (3)c是负数; (4)d不小于2的数.
练习:课本P.7中练习1.
归纳:根据不等式的意义,常用的不等号有下面的4种形式.
|
种类 |
符号 |
读法 |
举例 |
|
小于号 |
< |
小于 |
2+3<6,x<-4 |
|
大于号 |
> |
大于 |
2+3>5,x>-10 |
|
小于或等于号 |
≤ |
小于或等于(不大于) |
x≤8 |
|
大于或等于号 |
≥ |
大于或等于(不小于) |
x≥5 |
思考讨论:
例3 2006年2月5日扬州气象台预报本市气温是-2-4℃,这表示2月5日的最低气温是 ℃,最高气温是 ℃.设扬州市2月5日某一时刻气温为t℃,则关于t的不等量关系是 .
练习:(1)课本P.7练习2
(2)课本P.8习题7.1-2、3.
小结学习内容略.
拓展延伸:
1、 ;
2、 .
对自己所举出的例子用数学式子表示其中的数量之间的关系:
2、一只纸箱质量为1kg.当放入一些苹果(每个苹果的质量为0.25kg)后,箱子和苹果的总质量不超过10kg.
(1)填表:
|
苹果数 |
10 |
20 |
25 |
30 |
35 |
|
|
总质量/kg |
|
|
|
|
|
|
(2)估计这只纸箱内最多能装多少个苹果?
在日常生活中,同类量(如长度与长度,质量与质量,速度与速度)之间常常存在不等关系.
观察研究课本P.6“例如”:a 100.
“尝试”中,(1)x 2.9、y 3.1;(2)x+2 48.
交流:请你举出至少两个有不等关系实例,并与同学交流.
举例:1、 ;
1、小磊和他的妈妈、爸爸的体重分别为30kg、55kg和75kg. 春节期间,去瘦西湖游乐场玩跷跷板,小磊和妈妈玩时,谁会向上跷?若小磊和妈妈坐一头,爸爸坐在另一头时,谁会向上跷?
这说明:因为30kg 55kg(填写不等号),所以 会向上跷;
又因为30kg+55kg 75kg. (填写不等号),所以 会向上跷.
2.为学生创设学数学、用数学的情境,让学生体验用数学知识解决实际问题的方法.
重点和难点
重点:不等式的意义以及会用不等式表示不等关系;
难点:在实际问题中用不等式表示不等关系.
情境创设:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com