
2.为学生创设学数学、用数学的情境,让学生体验用数学知识解决实际问题的方法.
重点和难点
重点:不等式的意义以及会用不等式表示不等关系;
难点:在实际问题中用不等式表示不等关系.
情境创设:
1.在对实际问题的数量关系进行比较分析、作出推断的过程中,提高学生参与数学活动,乐于接触社会环境中数学信息的兴趣;
2.通过分析、抽象得到不等式的概念
情感态度目标:
1.引导学生分析具体事例,从对具体事例的分析中得到不等量关系;
2.会用不等式表示不等关系.
过程性目标:
1.在现实情境中认识数量间的不等关系,理解不等式的意义;
7.1生活中的不等式
目标要求:
5、一辆匀速行驶的汽车在10:20距离甲地40km,要在11:00之前驶过甲地,如果汽车速度为xkm/h,那么x应满足什么条件?
4、如图1-1,用两根长度均为l cm的绳子,分别围成一个正方形和圆.
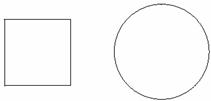
图1-1
(1)如果要使正方形的面积不大于25 cm2, 那么绳长l应满足怎样的关系式?
(2)如果要使圆的面积不小于100 cm2,那么绳长l应满足怎样的关系式?
(3)当l=8时,正方形和圆的面积哪个大?l=12呢?
(4)你能得到什么猜想?改变l的取值,再试一试.
3、用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C的含量及购买这两种原料的价格如下表:
|
原 料 维生素及价格 |
甲种原料 |
乙种原料 |
|
维生素C(单位/千克) |
600 |
100 |
|
原料价格(元/千克) |
8 |
4 |
(1)现配制这种饮料10千克,要求至少含有4200单位的维生素C,试写出所需甲种原料的质量x(千克)应满足的不等式.
(2)如果还要求购买甲、乙两种原料的费用不超过72元,那么你能写出x(千克)应满足的另一个不等式吗?
思路点拨:先弄清题意,找出不等关系。(1)至少含有4200单位的维生素C,所以600x+100(10-x)≥4200;(2) 费用不超过72元,所以8x+4(10-x)≤72.
易错辨析:(1)维生素C、原料的费用来源于甲、乙两种原料;(2) 10-x在解题中是一个整体,需加括号。
方法点评:解题时一定要搞清不等关系,以及每个数量的具体含义。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com