2．如果三角形有两边的长分别为5a，3a，则第三边x必须满足的条件是　　　　　　 ；

1．在△ABC中，∠A －∠C ＝ 25°，∠B －∠A ＝ 10°，则∠B ＝　　 ；

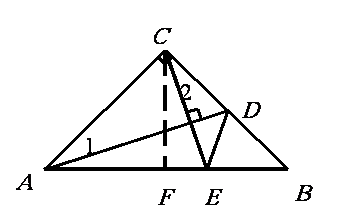
如图，等腰直角三角形ABC中，∠ACB＝90°，AD为腰CB上的中线，CE⊥AD交AB于E．求证∠CDA＝∠EDB．

提示：

作CF⊥AB于F，

则∠ACF＝45°，

在△ABC中，∠ACB＝90°，CE⊥AD，

于是，由∠ACG＝∠B＝45°，AB＝AC ，

且易证∠1＝∠2，

由此得△AGC≌△CEB(ASA)．

再由CD＝DB，CG＝BE，∠GCD＝∠B，

又可得△CGD≌△BED(SAS)，

则可证∠CDA＝∠EDB．

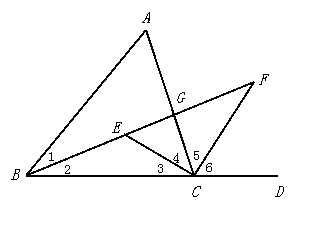
五 如图，△ABC中，∠1＝∠2，∠3＝∠4，∠5＝∠6．∠A＝60°．求∠ECF、∠FEC的度数．

略解：因为 ∠A＝60°，

所以 ∠2+∠3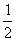＝(180°－60°)＝60°；

又因为 B、C、D是直线，

所以 ∠4+∠5＝90°；

于是 ∠FEC＝∠2+∠3＝60°，

∠FCE＝∠4+∠5＝90°，

∠FEC＝60°．

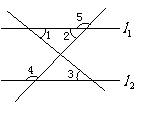
六 在Rt△ABC中，∠A＝90°，CE是角平分线，和高AD相交于F，作FG∥BC交AB于G，求证：AE＝BG．

略解：作EH⊥BC于H，

由于E是角平分线上的点，可证 AE＝EH ；

且又由 ∠AEC＝∠B+∠ECB＝∠CAD+∠ECA＝∠AFE

可证 AE＝AF，

于是由 AF＝EH，∠AFG＝∠EHB＝90°，∠B＝∠AGF．

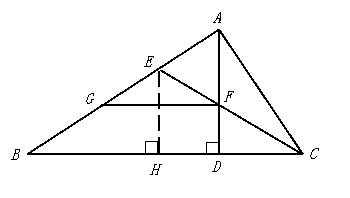可得 △AFG≌△EHB；

所以 AG＝EB，

即 AE+EG＝BG+GE，

所以 AE＝BG．

10.填写理由:

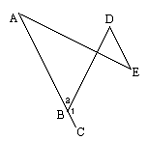已知：如图8,ABC是直线,∠1=115°,∠D=65°.

　求证：AB∥DE.

　证明：∵ABC是一直线,(已知)

∴∠1+∠2=180°(　　　　　　　　　 )

∴∠2=65°

又∵∠D=65°(已知)

∴∠2=∠D

∴　　 ∥　　 (　　　 　　　　　　　)

9. 如图,下列条件中不能得出两直线平行 的是(　　 )．　　　　

A.∠2=∠6　　　　 B.∠3+∠5=180º　　　　　　　　

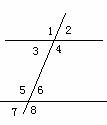C.∠4+∠6=180º　　 D.∠2=∠8　　　　　　　　　

8.在同一平面内两条直线的可能位置是　　　　　 (　　 )．

A.平行　　 B.相交　　 C.平行或相交　　 D.既不平行也不相交

7.如图6, 已知: ∠3＝∠4, 则　　 (　　 )．

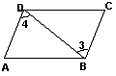
图6

A.DC∥AB　　 B.AD∥BC且AB∥DC　　 C.都不平行　　 D.AD∥BC

6.(淄博市2004年)如图，下列条件中，能判断直线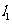//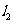的是

A.∠2=∠3

B.∠1=∠3

C.∠4+∠5=180°

D.∠2=∠4

5.如图5，下列说法中，错误的是　　　　 (　　 )．

A.∠1与∠3是同位角　　　　 B.∠2与∠3是内错角

C.∠1与∠4是同旁内角　　 D.∠3与∠4是同旁内角

4. 如图4, 已知BE平分∠ABD, DE平分∠BDC, 并且∠1+∠3＝90°, 则　　 ∥　　 .理由是　　　　　　　　　　　　　　　　 .

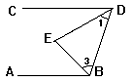
图4　　　　　　　　 图5