
6.已知等腰三角形的一边长等于12cm,腰长是底边长的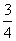 ,求它的周长。
,求它的周长。
5.在△ABC中,①∠A+∠B=∠C,则△ABC为什么三角形?②若2∠A=3∠B=4∠C,则△ABC为什么三角形?
4.等腰三角形的两个角的比为1:4,则顶角的度数为多少?
3.在等腰三角形中,顶角的邻补角等于底角的多少倍?
2.等腰三角形的两条边的长分别为4和9,则这个三角形的腰长是多少?底边长为多少?
1.在等腰三角形ABC中,AB的长是AC的2倍,三角形的周长是40,则AB是多少?
2.会求特殊三角形的边与角
难点:等腰三角形边、角的计算及分类讨论思想的应用。
[讲一讲]
例1:已知:如图,在以AC为底边的等腰△ABC中,AB=10,在以AD为底边的等腰△ACD中,CD=7,求三角形ABC的周长
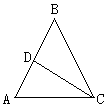
分析:根据题意可以画出图形,再根据等腰三角形特殊的性质,腰相等,求出△ABC中AB与AC及BC的长,间接求周长,
解:∵△ABC为等腰三角形,且AC为底边,∴AB=BC=10
∵△ACD为等腰三角形,且AD为底边,∴AC=CD=7
∴△ABC的周长C=AB+BC+AC=10+10+7=27
例2:一个等腰三角形的周长为18cm。
(1)已知腰长是底边长的2倍,求各边长。
(2)已知其中一边长为4cm,求其它两边长。
分析:区别(1)与(2)的问法,(1)中指出了腰长为底边的2倍,则用方程思想,设未知数,再将三角形表示出来即可求。而(2)中只说其中一边长为4cm,在等腰三角形中,一边可以是底边也可以是腰,因此就有两种答案了,但还要注意在求出结果后,需要验证一下所求的三角形是否成立。
解:
1)设底边长为xcm,则腰长为2xcm。
∴x+2x+2x=18 ∴x=3.6 2x=7.2
∴三边长分别为3.6cm、7.2cm和7.2cm
2)①若4cm为底,设腰长为xcm
∴2x+4=18 ∴x=7
②若4cm为腰,设底边长为xcm
∴x+4×2=18 ∴x=10
∵4+4<10不满足三角形的定义
即两边之和小于等三边 故4cm不能为腰
∴三角形其它两边长为7cm和7cm
例3:已知:在△ABC中,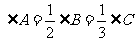 ,试判断△ABC为什么三角形?
,试判断△ABC为什么三角形?
分析:利用三角形内角和及方程思想可求三角形的三个内角,从而判断△ABC的形状
解:∵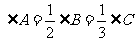 ∴∠B=2∠A
∠C=3∠A
∴∠B=2∠A
∠C=3∠A
∵∠A+∠B+∠C=180° ∴∠A+2∠A+3∠A=180°
∴6∠A=180°∴∠A=30° ∴∠B=60°,∠C=90°
∴△ABC为直角三角形
例4:等腰三角形的周长为21cm,一腰上的中线把这个三角形分成周长相差3cm的两个三角形,求等腰三角形各边的长
分析:如图△ABC中,AB=AC,D为AC中点,根据题意有AB+AC+BC=21cm,还有一个已知条件是:一腰上的中线把三角形分成周长相差3cm的两个三角形。
即AB+BD+AD与BD+DC+BC相差3cm,但没有说明△ABD周长大还是△BCD周长大,于是此题也应该注意进行分类讨论。
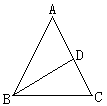
解:①AB+BD+AD-(BD+DC+BC)=3
∴AB+AD-DC-BC=3 ∵AD=DC ∴AB-BC=3又2AB+BC=21
∴AB-3+2AB=21 ∴3AB=24 ∴AB=8cm ∴BC=8-3=5
②BD+DC+BC-(AB+BD+AD)=3∴BC-AB=3
又2AB+BC=21 ∴2AB+AB+3=21
∴3AB=18 ∴AB=6 ∴BC=9
∴等腰三角形各边长为5cm、8cm、8cm或9cm、6cm、6cm
[同步达纲练习]
1.掌握三角形的分类方法
①按边分类:

②按角分类:

3.求以1995的质因数为边的三角形共多少个?

2.三角形三边长均为整数a,b,c,且a≤b≤c.若b=5,求出所有合条件的三角形的另两边a,c,合条件三角形共多少个?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com