
3.判断正误:
(1)三角形的三条角平分线,中线,高线均在三角形内部
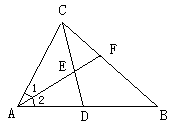
(2)如图,AD=BD,∠1≠∠2,则CE是△ABC的中线,AE是△ABC的角平分线
(3)三角形的内角与外角互补( )
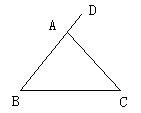
(4)如图,∠DAC是∠BAC的外角
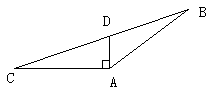
(5)如图,AD是△ABC的高( )
(6)AE是△ABD的高( )
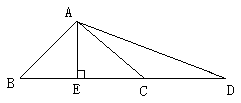
2.下图中有几个直角三角形?并说出名称
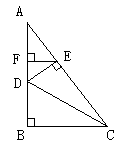
已知:AB⊥BC DE⊥AC EF⊥AB
1.做出钝角三角形的高,并注明垂心的位置
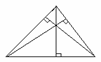
3.高线:由三角形一个顶点向它的对边画垂线,顶点和垂足间的线段,简称为“三角形的高”,三条高线的交点叫做垂心。
图形:
|
|
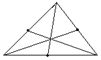
锐角三角形 |
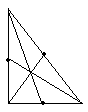
直角三角形 |
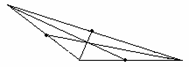
钝角三角形 |
小结 |
|
角平分线 |
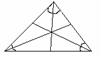 |
 |
 |
交点均在内部 |
|
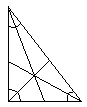
重线 |
 |
 |
 |
交点均在内部 |
|
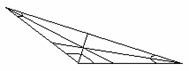
高线 |
 |
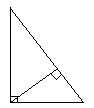 |
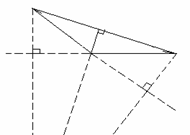 |
交点位置不同 |
例2:下图中有几个三角形,并说出名称
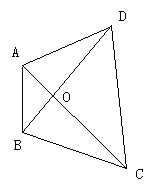
分析:任意不在同一条直线上的三个点就可以确定一个三角形
解:共有8个△ABO △BOC △COD △DOA △ABC △BCD △CAD △DAB
例3:已知:BE是△ABC的中线,DF是△ADE的中线AC=8cm,求EF
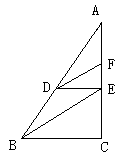
分析:由三角形中线的定义可知,三角形边上的中点,利用线段中点定义可求EF
解:∵BE是△ABC的中线
∴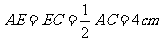
∵DF是△ADE的中线,∴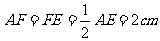
∴EF为2cm
[同步达纲练习]
2.中线:在三角形中,连结一个顶点和它的对边中点的线段,三条中线的交点叫做重心
1.角平分线:三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线,三条角平分线的交点叫做内心
1.三角形中三线的画法,特别是它们的共同点与不同点
[讲一讲]
例1:总结三角形中的重要元素及重要线段
在△ABC中,元素
①边,线段AB,BC,AC,也可记为a,b,c边
②顶点:点A B C
③内角,∠ABC ∠BAC ∠ACB
④外角,∠ABF ∠CAE ∠ACD
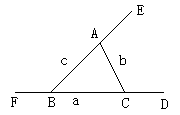
重点线段
1.三角形中基本概念和重要的线段
难点:
8.等腰三角形一腰上的中线将其周长分为15和12两部分,求三角形各边长。
7.一个等腰三角形的两外角的比为1:4,求底角的外角的度数。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com