
5.如图7-1-6,AD⊥BC于D,CE⊥AB于E,AD、CE交于点O,OF⊥CE,则下列说法中正确的是………………………………………………………………………………………………( )
A.OE为△ABD中AB边上的高 B.OD为△BCE中BC边上的高
C.AE为△AOC中OC边上的高 D.OF为△AOC中AC边上的高
4.下列图形具有稳定性的是……………………………………………………………( )
A.正方形 B.梯形 C.三角形 D.平行四边形
3.下列说法中,正确的是………………………………………………………………( )
A.三角形的角平分线是射线
B.三角形的高总在三角形的内部
C.三角形的高、中线、角平分线一定是三条不同的线段
D.三角形的中线在三角形的内部
2.下列各组线段中能组成三角形的是…………………………………………………( )
A.a=6,b=8,c=15 B.a=7,b=6,c=13
C.a=4,b=5,c=6
D.a=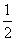 ,b=
,b=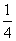 ,c=
,c=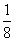
1.三角形的一条高是一条………………………………………………………………( )
A.直线 B.垂线 C.垂线段 D.射线
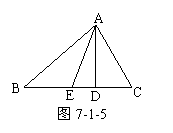
4.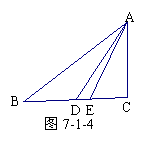 如图7-1-5,以AD为高的三角形共有 .
如图7-1-5,以AD为高的三角形共有 .
 慧眼识金
慧眼识金
3.如图7-1-4,AD是△ABC的中线,AE是△ABC的角平分线,若BD=2cm,则BC= ;若∠BAC=600,则∠CAE= .
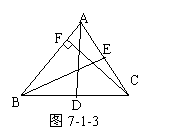
2.如图7-1-3,AD是△ABC的角平分线,则∠
=∠ =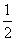 ∠ ;E在AC上,且AE=CE,则BE是△ABC的 ;CF是△ABC的高,则∠ =∠ =900,
∠ ;E在AC上,且AE=CE,则BE是△ABC的 ;CF是△ABC的高,则∠ =∠ =900,
CF AB.
1.AD是△ABC的高,可表示为 ,AE是△ABC的角平分线,可表示为 ,BF是△ABC的中线,可表示为 .
7.1与三角形有关的线段

 [例1]如图7-1-1,已知△ABC中,AB=AC,周长为16cm,AC边上的中线BD把△ABC分成周长差为2cm的两个三角形,求△ABC的各边长.
[例1]如图7-1-1,已知△ABC中,AB=AC,周长为16cm,AC边上的中线BD把△ABC分成周长差为2cm的两个三角形,求△ABC的各边长.
[点拨]本题渗透着分类思想,应考虑要大于底边或腰长小于底边
两种情况(即周长之差为2),同时还要注意求得的三角形三边长是否
符合题意,这是我们在后面要学到的,本题的两种结果都符合要求,
这一点将在后面讨论.
[答案]∵AD=DC
(1)当△ABD的周长-△DBC的周长=2cm时,则(AB+BD+AD)-(BC+BD+CD)
=AB-BC+(BD-BD)+AD-CD)=AB-BC=2.又∵AB+BC+AC=16,且AB=AC,
故2AB+BC=16,∴AB=6,BC=4.此时,△ABC的各边长AB=AC=6cm,bc=4cm.
(2)当△BDC的周长-△ABD的周长=2cm时,有BC-AB=2,又2AB+BC=16,
∴AB=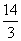 ,BC=
,BC=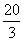 .此时,△ABC的各边长为AB=AC=
.此时,△ABC的各边长为AB=AC=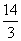 ,BC=
,BC=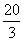
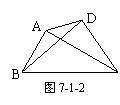
[例2]四边形的两条对角线长之和一定小于其周长吗?
 [点拨]作四边形的对角线,可得到若干个三角形,这样可以把四边形的问题转化为三角形的问题,并归结为“三角形的三边关系”.
[点拨]作四边形的对角线,可得到若干个三角形,这样可以把四边形的问题转化为三角形的问题,并归结为“三角形的三边关系”.
|
理由:如图7-1-2,在△ABD中,必有AB+AD>BD;在△BDC中,必有BC+CD>BD;
所以AB+BC+CD+DA>2BD,同理,AB+BC+CD+DA>2AC;故2(AB+AC+CD+DA)>2(AC+BD)
∴AB+BC+CD+DA>AC+BD,即AC+BD<AB+BC+CD+DA.

 画龙点睛
画龙点睛
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com