3.三角形三边有怎样的不等关系?

　　 通过动手实验同学们可以得到哪些结论?

　　 三角形的任意两边之和大于第三边;任意两边之差小于第三边.

2.在同一个三角形中,任意两边之差与第三边有什么关系?

1.在用一个三角形中,任意两边之和与第三边有什么关系?

　　 画出一个△ABC,假设有一只小虫要从B点出发,沿三角形的边爬到C,它有几种路线可以选择?各条路线的长一样吗?

　　 同学们在画图计算的过程中,展示议论,并指定回答以上问题:

　　 (1)小虫从B出发沿三角形的边爬到C有如下几条路线.

　　 a.从B→C

　　 b.从B→A→C

　　 (2)从B沿边BC到C的路线长为BC的长.

　　 从B沿边BA到A,从A沿边C到C的路线长为BA+AC.

　　 经过测量可以说BA+AC>BC,可以说这两条路线的长是不一样的.

2.板书:在黑板上老师画出以下几个图形.

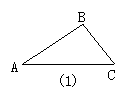
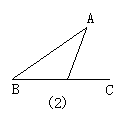
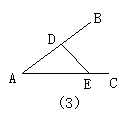
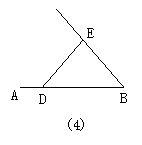
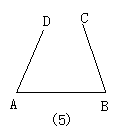
　　 (1)教师引导学生观察上图:区别三条线段是否存在首尾顺序相接所组成的.图(1)三条线段AC、CB、AB是否首尾顺序相接.(是)

　　 (2)观察发现,以上的图,哪些是三角形?

　　 (3)描述三角形的特点:

　　 板书:“不在一直线上三条线段首尾顺次相接组成的图形叫做三角形”.

　　 教师提问:上述对三角形的描述中你认为有几个部分要引起重视.

　　 学生回答:

　　 a.不在一直线上的三条线段.

　　 b.首尾顺次相接.

1.投影:图形见章前P68-69图.

　　 教师叙述: 三角形是一种最常见的几何图形之一.(看条件许可, 可以把古埃及的金字塔、飞机、飞船、分子结构……的投影,给同学放映)从古埃及的金字塔到现代的飞机、上天的飞船,从宏大的建筑如P68-69的图,到微小的分子结构, 处处都有三角形的身影.结合以上的实际使学生了解到:我们所研究的“三角形”这个课题来源于实际生活之中.

　　 学生活动:(1)交流在日常生活中所看到的三角形.

　　 (2)选派代表说明三角形的存在于我们的生活之中.

1.如图(3.9-8)，某铁路MN和公路PQ相交于点O，且交角为90°,某仓库G在A区，到公路、铁路距离相等(即G在∠NOQ的平分线上)，且到公路与铁路的相交点O的距离为200m.

(1)在图上标出仓库G的位置(比例尺1∶10000,用圆规作图，保留作图痕迹，不写作法)：

(2)求出仓库G到铁路的实际距离.

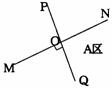
图3.9-8

2.△ABC中，AB=BC=CA，三内角平分线交于O，OP⊥AB于P，OM⊥BC于M，ON⊥CA于N，AH⊥BC于H.求证OP+OM+ON=AH.

[生活实际运用]

1.如图3.9-7，AB=AC，AD=AE，BD、CE交于O，求证AO平分∠BAC.

图3.9-7