4、你认为图4的图形具有稳定性吗？

3、如图3，在△ABC中∠BAC=60度，∠B=45度，AD是∠BAC的角平分线，求∠ADB的度数。

2、AE是△ABC的中线，那么BE=　　 =　　 BC

1、AD是△ABC的角平分线，那么∠BAD=　　 =　　　

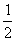
4、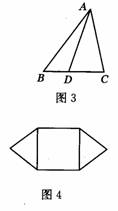高的交点有何特别之处？

通过实际操作，小组合作，让学生真切地体会三线关系。

3、你认为“三线”定义中，高与线段垂线、三角形角平分线与角的平分线、中线与线段中点有何异同？

　　 问题：1、你认为一个三角形有几条高，几条中线，几条角

平分线？并分别作出来．

2、通过本组作出的三线，请说明它们各自的共性．

3、多媒体播放天花板三角形框架、起重机三角形吊臂、

屋顶三角形钢架、钢架桥中三角形．

　　 问题：(1)你能观察到这些结构的特点吗？

　　　　　 (2)你解释一下为何要做这样的结构．

2、如图2，教师再给出一个三角形纸片，对折，使AC与AB所在直线重合，折痕与BC交于D.

　　 问题：(1)通过这个操作你认为AD有什么位置特点？

　　　　　 (2)你能用尺规作出AD吗？

　　　　　 (3)请给出三角形角平分线的定义．

中线的概念

1、如图1，教师给出一个准备好的三角形纸片，把B,C重合对折，折痕与BC交于点D.

问题：(1)D点有什么特殊性？

　　 (2)连接线段AD，AD把△ABC分成的两个三角形的面积有何关系？

　　　 (3)请归纳线段AD的特点．

　　　 (4)你能用尺规作出中线AD吗？

　　 并用语言描述中线定义．