
本节课是在小学初步认识三角形的基础上,又具体介绍了三角形的有关概念和三角形三边的,初步了解了一些简单几何体和平面图形及其基本特征,会简单的说理.三角形的高、中线、角平分线分别与已学过的垂线、线段的中点、角的平分线有关.它既是上学期所学线段、角、相交线以及平行线等知识的延续,又是后继学习内切圆及等腰三角形等知识的基础.在知识体系上具有承上启下的作用.
《数学课程标准》指出:“有意义的学习活动不能单纯地依赖模仿和记忆”.动手实践、自主探究、合作交流是学习数学的重要方式.为了充分体现新课标的要求,培养学生的动手实践能力、逻辑思维能力,因此本节课的设计上充分让学生从生活中体验数学的无处不在,运用数学无时不有,激发学生的学习兴趣,自然地将学生的思维引入本节课的学习重点,顺利的突破难点,为学生的有效思维营造一个广阔的空间.从而实现人人学有价值的数学,人人都能获得必需的数学,不同的人在数学上得到不同的发展.
基于上述分析,结合学生已有的认知水平的年龄特征,制定本节如下的教学目标:
(1)知识与技能目标:通过观察、画、折等实践操作、想像、推理、交流等过程,认识三角形的高线、角平分线、中线;会画出任意三角形的高线、角平分线、中线,通过画图、折纸了解三角形的三条高线所在直线、三条角平分线、三条中线会交于一点.
(2)过程与方法目标:经历画、折等实践操作活动过程,发展学生的空间观念,推理能力及创新精神.学会用数学知识解决实际问题能力,发展应用和自主探究意识,并培养学生的动手实践能力.
(3)情感与态度目标:通过对问题的解决,使学生有成就感,培养学生的合作精神,树立学好数学的信心.
2、选做题:
(1)一个三角形有 条中线、 条角平分线。
(2)任意三角形三条中线、角平分线都在三角形 部。
(3)直角三角形ABC中,∠C=90度,∠A=40度,BD是∠ABC的角平分线,则∠CDB=
[教学反思]
本课题设计思路按操作、猜想、验证的学习过程,遵循从感性到理性的渐进认识规律,暴露了知识发生过程,体现了数学学习的必然性.教学先从学生折纸开始,让学生体验三角形中线、角平分线的存在及其性质,而后通过尺规作图,加深学生对中线、角平分线的认识,增加了数学学习兴趣.讲三角形高时,学生也想用折纸折出三角形高,结果碰到困难(钝角三角形),使新、旧知识大碰撞,加速知识同化.在探究三角形稳定性时,课堂出现很多三角形结构,并让同学解释,使学生认识到数学来源于生活同时数学也服务于生活的真谛,增强学生
学习数学的热情,整堂课都以学生操作、探究、合作贯穿始终,培养学生动手、合作、概括能力.
1、必做题:教科书75页习题7.1第4、5题。
3、角形为什么具有稳定性,要求学生能验证、操作、用自己的语言叙述.
2、三线定义.
1、请小组同学回忆一下本课主要内容,由师生共同用较准确语言描述.
3、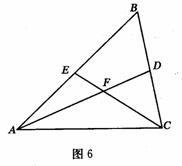 请举出生活中利用三角形稳定性的例子。
请举出生活中利用三角形稳定性的例子。
2、如图6,△ABC的角平分线AD、CE相交于点F,设∠B=α,请你用α的式子表示∠AFC的度数。
1、如图5,D、E分别是△ABC的边AC、BC的中点,下列说法正确吗?
(1) DE是△BDC的中线。
(2) BD是△ABC的中线
(3) AD=CD、BE=EC
(4) ∠C的对边是DE。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com