[总结]

1、 本节课学习的数学知识：

“三线八角”、同位角的概念以及“同位角相等，两直线平行”

类型之一　 直接运用

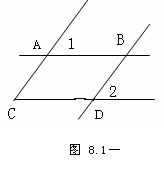
例1、如图8.1-10所示：∠1=∠C，∠2=∠C请你找出图中互相平行的直线，并说明理由

[思路分析]在图中找到∠1，∠C，∠2的位置，易知∠1，∠C是同位角，∠C，∠2是同位角，于是由“同位角相等，两直线平行.”可知，AB∥CD

解：(1)AB∥CD

因为∠1与∠C是 ABCD 被AC截成的同位角, 且∠1 =∠C

所以 AB∥CD

(2)AB∥CD.

因为∠2与∠C是BDAC被CD截成的同位角且∠2=∠C所以AC∥BD

[点评]运用“同位角相等,两直线平行”是判定两条直线平行的有效方法.

类型之二　 间接运用

例2、如图8.1-11直线a、b被直线c所截，∠1=35°，

∠2=145°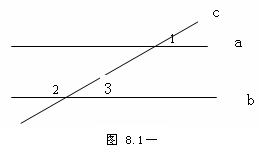，问：直线a与b平行吗？

[思路分析]考虑到要运用“同位角相等，两直线平行.”来判断两直线是否平行，而所给一角是∠1=35°.∠2=145°，于是可以由∠2=145°求得∠3=35°，则可知结果.

解：因为∠2=145°，∠2+∠3=180°，所以有∠3=35°，而∠1=35°，则∠1=∠3.

　 所以a//b.

[点评]在图形中准确地找到必需同位角是解题的前提.

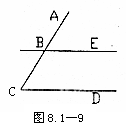
2、如图8.1-9，

∠C=31°，当∠ABE=　　 度时，就能使BE//CD？

答案：31°

1、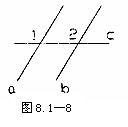如图8.1-8，

∠1=150°，

∠2=150°，

a//b吗？

答案：由于∠1=150°，

∠2=150°，则有∠1=∠2，则有a//b

3、两直线平行条件

[讨论]

如图，两条直线被第三条直线所截，转动直线b，当直线b转动到不同的位置时，从的大小变化说出这两条直线的位置关系.

在这个过程中，存在着一个平行的位置关系，那么与有何关系时，这两条线平行呢？

[双向沟通]

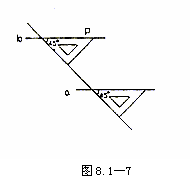我们在用三角板平推法画平行线时还发现：画平行线仍借助了第三条直线，但是要用与a、b都相交的第三线，根据“三线八角”的名称，在画平行线的过程中，实际上是保证了同位的两个角都是45⁰，从而得出：两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行.可以简单说成：同位角相等，两直线平行.

[议一议]

2、认识同位角的注意点

看两个角是不是同位角，

(1)　　 看它们是不是在一条直线的同侧，

(2)　 看截它们的两条直线是什么，这两个角是不是在截它们的直线的同旁.

也就是说，是否满足“F”型.

1、认识同位角

[画一画]两条直线AB、 CD与直线EF相交，交点分别为E F

如图8.1-4则称直线AB 、CD 被直线EF所截，直线EF为截线.

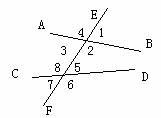
　　　　　 图8.1-4

[说一说]二条直线AB 、CD 被直线EF所截可得8个角，即所谓“三线八角”.

　 这八个角中对顶角、邻补角各有哪些？

[双向沟通]这八个角中有对顶角：∠1与∠3，∠2与∠4，∠5与∠7，∠6与∠8.

　 邻补角有：∠1与∠2，∠2与∠3，∠3与∠4，∠5与∠6，∠6与∠7，∠7与∠8，∠8与∠5.

[感悟]

同位角：两条直线被第三条直线所截，在二条直线的同侧，且在第三条直线的同旁的二个角叫同位角.

如图中的∠1与∠5分别在直线AB、 CD的上侧，又在第三条直线EF的右侧，所以∠1与∠5是同位角，它们的位置相同，在图中还有∠2与∠6，∠4与∠8，∠3与∠7也是同位角.

[做一做]

如图8.1-5中，同位角各有多少对？

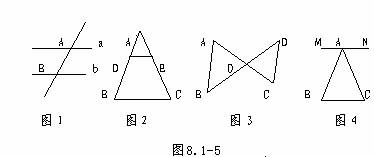
答案：(1)4；(2)4；(3)4；(4)0；

导语一

　垂直的定义可以作为判断两条相交直线是否垂直的方法，那么平行线的定义能否作为判断两条直线是否平行的方法呢？如果能的话，我们用平行线的定义来判断两条直线平行要满足什么条件？

导语二

情境一(苏教版七年级下)

下面两种两条直线的位置，可以通过观察发现，当我们不能用定义来判断两条直线平行时，就要寻找另外一些判定两直线平行的方法.

图8.1-1

情境二(人教版七年级下)

如图8.1-2,观察：∠1与∠2相等，所画的直线a、b平行吗？

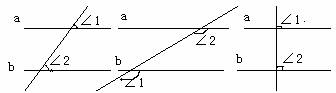
图8.1-2

情境三\

如图8.1-3.∠1与∠2不相等，所画的直线a、b平行吗？

　　　　　　　　 图8.1-3

导语三

大家还记得画平行线的方法吗？那为什么要平推呢？这里有什么数学道理吗？让我们一起来研究今天的课题.

板书课题：探索直线平行的条件

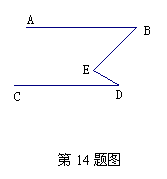
14.已知：如图，AB、BE、ED、CD依次相交于B、E、D，∠E＝∠B+∠D.

试说明AB∥CD.

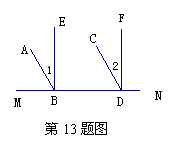
13.如图已知∠1＝∠2，再添上什么条件，可使AB∥CD成立？并说明理由.