
2.培养学生简单的合情说理能力.
1.进一步探索直线平行的条件以及内错角、同旁内角的特征过程.
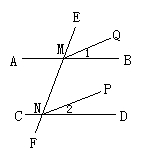
6、如图8.1-19,已知直线AB、CD被直线EF所截,如果∠BMN=∠DNF,∠1=∠2,
那么MQ∥NP,为什么?
 .
.
图8.1-19
解析:由于∠BMN=∠DNF,∠1=∠2
则∠BMN+∠1=∠DNF+∠2
即∠QMN=∠PNF,MQ∥NP
5、如图8.1-18,在同一平面内,如果两条直线b、c都垂直于同一条直线a,那么这两条直线平行吗?为什么?
解析:因为a⊥b,c⊥a,
所以∠1=90°,∠2=90°.
则∠1=∠2=90°,
从而b∥c (同位角相等,两直线平行).
4、如图8.1-17,指出∠B,∠C,∠1的同位角.
解析:依据同位角的意义,可知
∠B的同位角有:∠AED,∠3,∠EDC;
∠C的同位角有:∠AFD,∠1,∠BDF;
∠1的同位角有:∠1;
3、如图8.1-17,若∠A=_____,
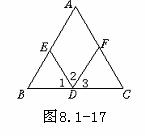 则AC∥ED ,这是因为________
则AC∥ED ,这是因为________

解析:∠BED,同位角相等,两直线平行
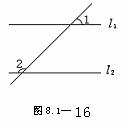
2、如图8.1-16若∠1=45°,则∠2=_____时. l1∥l2,
解析:要使得l1∥l2,则必须有同位角相等,则∠2=135°
1、如图8.1-15,点E在CD上,点F在BA上,G是AD延长线上一点.
若∠A=∠1,则可判断_______∥_______,因为________.
解析:(1)CD∥AB, 同位角相等,两直线平行
2、如何判定两条直线平行?
[拓展]
类型之三 识别复杂图形中的同位角
例3、如图8.1-12 (1)DE为截线,∠E与哪个角是同位角?
(2)∠B与哪个角是同位角?截出这两个角的是哪两条直线与被哪条直线所截?
(3)∠B和∠E是同位角吗?为什么?
[思路分析]看两个角是不是同位角,首先是看它们是不是在一条直线的同侧,然后在看,截它们的两条直线是什么,这两个角是不是在截它们的直线的同旁.也就是说,是否满足“F”型.
解:(1) ∠E与∠3是同位角
(2) ∠B与∠3是同位角,截出这两个角的截线是直线ED,被截线是直线EF、BC.
(3)不是.因为∠B与∠E的边没有落在同一直线上.不属于‘三线八角’中的角, 所以∠B和∠E不是同位角.
 [点评]判别两个角是否为同位角就是根据它的意义,抓住其本质:是否在一条直线的同侧且满足“F”型.
[点评]判别两个角是否为同位角就是根据它的意义,抓住其本质:是否在一条直线的同侧且满足“F”型.
变式题:
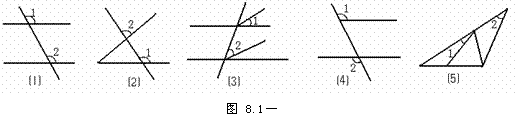
图8.1-13中∠1和∠2是同位角的是( )
A. ⑴、⑵、⑶, B. ⑵、⑶、⑷,
C. ⑶、⑷、⑸, D. ⑴、⑵、⑸
 答案:D
答案:D
类型之四 由同位角相等判别平行线的说理
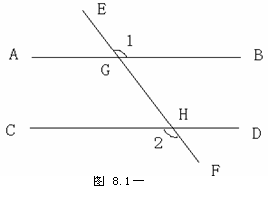
例4、如图所示,直线AB、CD被EF所截,且∠1=∠2,则AB//CD,为什么?
[思路分析]依据“同位角相等,两直线平行”,看有没有同位角相等.
解:注意到∠GHD与∠2是对顶角,则有∠GHD=∠2
又因为∠1=∠2,所以∠1=∠GHD
根据“同位角相等,两直线平行”,可知AB//CD
 [点评]“同位角相等,两直线平行”是判定两直线平行的有用工具.
[点评]“同位角相等,两直线平行”是判定两直线平行的有用工具.
2、 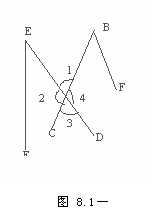 本节课学习的数学方法:
本节课学习的数学方法:
(1)转化思想.
(2)运用“同位角相等,两直线平行”判定两条直线平行.
[反思]1、什么是“三线八角”?什么样的角才能称得上是同位角?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com