1、在Rt△ABC中，∠C＝90°，AC＝1，AB＝3，

则tanA＝________，tanB＝______.

5、思考与探索三：

怎样计算任意一个锐角的正切值呢？

(1)例如，根据下图，我们可以这样来确定tan65°的近似值：当一个点从点O出发沿着65°线移动到点P时，这个点向右水平方向前进了1个单位，那么在垂直方向上升了约2.14个单位.于是可知，tan65°的近似值为2.14.

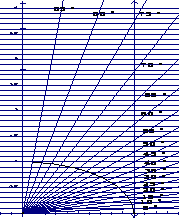(2)请用同样的方法，写出下表中各角正切的近似值.

(3)利用计算器我们可以更快、更精确地求得各个锐角的正切值.

(4)思考：当锐角α越来越大时，α的正切值有什么变化？

___________________________________________________________.

4、牛刀小试

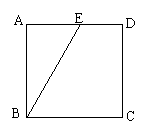
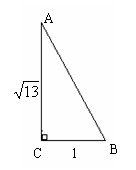根据下列图中所给条件分别求出下列图中∠A、∠B的正切值.

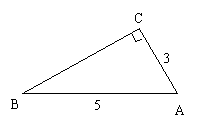
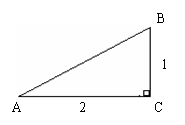
(通过上述计算，你有什么发现？_____________________________________.)

3、正切的定义

如图，在Rt△ABC中，∠C＝90°，a、b分别是∠A的对边和邻边.我们将∠A的对边a与邻边b的比叫做∠A_______，记作______.

即：tanA＝________＝__________

(你能写出∠B的正切表达式吗？)试试看.

2、思考与探索二：

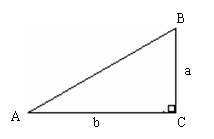
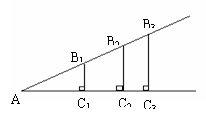
(1)如图，一般地，如果锐角A的大小已确定，我们可以作出无数个相似的Rt△AB₁C₁，Rt△AB₂C₂，Rt△AB₃C₃……，那么有：Rt△AB₁C₁∽________∽________……

根据相似三角形的性质，得：

＝_________＝_________＝……

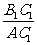(2)由上可知：如果直角三角形的一个锐角的大小已确定，那么这个锐角的对边与这个角的邻边的比值也_________.

1、思考与探索一：

如何描述台阶的倾斜程度呢？

①　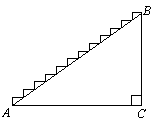　 可通过测量BC与AC的长度，再算出它们的比，

来说明台阶的倾斜程度.

(思考：BC与AC长度的比与台阶的倾斜程度有何关系？)

答：_________________________________________.

②讨论：你还可以用其它什么方法？能说出你的理由吗？

答：_________________________________________.

2. 问题：下列图中的两个台阶哪个更陡？你是怎么判断的？

⑴如图，一把梯子斜靠在墙上，当它的顶端向下滑动后，它的底端将如何运动？滑动前(图中AB)与滑动后(图中A′B′)的位置的梯子，哪一个更陡些？你是根据什么判断的？你能用语言向同学描述吗？

　 ⑵如何描述梯子在两个不同位置的具体的倾斜程度呢？

提示：在这一过程中变化的量有哪些？如何变化的？

⑶如图，如果两把梯子AB、CD靠在墙上，且AB∥CD，

这两把梯子的倾斜程度相同吗？前面所提到的描述倾斜程

度的量在这里分别对应相同吗？你能说明理由吗？

1. 观察：如图，是某体育馆为了方便不同需求的观众，

该体育馆设计了多种形式的台阶.

7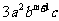．是六次单项式，则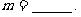

6．关于m的多项式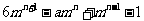是三次三项式，则，