
45.解析:要想BE与DF平行,就要找平行的条件.题中只给出了∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC.那么我们是利用同位角相等呢还是利用同旁内角互补?经过仔细观察图形我们知道∠BFD是三角形ADF的外角,则∠BFD=∠A+∠ADF.而∠ADF是∠ADC的一半,∠ABE是∠ABC的一半,所以我们选择用同旁内角互补来证平行.
解:BE与DF平行.理由如下:
由n边形内角和公式可得四边形内角和为(4-2)×180°=360°.
因为∠A=∠C=90°,
所以∠ADC+∠ABC=180°.
因为BE平分∠ABC,DF平分∠ADC,
所以∠ADF=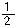 ∠ADC,∠ABE=
∠ADC,∠ABE=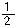 ∠ABC.
∠ABC.
因为∠BFD是三角形ADF的外角,
所以∠BFD=∠A+∠ADF.
所以∠BFD+∠ABE=∠A+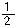 ∠ADC+
∠ADC+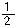 ∠ABC=∠A+
∠ABC=∠A+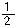 (∠ADC+∠ABC)=90°+90°=180°.
(∠ADC+∠ABC)=90°+90°=180°.
所以BE与DF平行.
44.解析:在第(1)和第(2)问中,没有说明所给边长是腰长还是底边长,因此我们要进行分类讨论.在第(3)问中,只给出了三边长都是整数,而此三角形又是等腰三角形,所以其最长边小于8cm,我们可以用列表法一一列出各组边长.
解:(1)如果腰长为4cm,则底边长为16-4-4=8cm.三边长为4cm,4cm,8cm,不符合三角形三边关系定理.所以应该是底边长为4cm.所以腰长为(16-4)÷2=6cm.三边长为4cm,6cm,6cm,符合三角形三边关系定理,所以另外两边长都为6cm.
(2)如果腰长为6cm,则底边长为16-6-6=4cm.三边长为4cm,6cm,6cm,符合三角形三边关系定理.所以另外两边长分别为6cm和4cm.
如果底边长为6cm,则腰长为(16-6)÷2=5cm.三边长为6cm,5cm,5cm,符合三角形三边关系定理,所以另外两边长都为5cm.
(3)因为周长为16cm,且三边都是整数,所以三角形的最长边不会超过8cm且是等腰三角形,我们可用列表法,求出其各边长如下:
7cm,7cm,2cm;6cm,5cm,5cm;6cm,6cm,4cm,共有这三种情况.
43.解析:本题要求AC与AB的边长的差,且AC与AB的长度都不知道,不少同学感到无从下手.其实,只要我们仔细分析分析题中条件:三角形ABD的周长比三角形ACD的周长小5,即AC-AB+CD-BD=5,又AD是BC边上的中线,所以BD=CD.所以AC-AB=5.
解:AC-AB=5.
42.解析:本题已知一边长和三条高,我们可以利用三角形的面积公式求得另外两边长,三边相加即可得到三角形的周长.
解:由三角形面积公式可得S△ABC=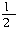 BC×AD=
BC×AD=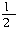 AC×BE,即16×3=4×AC,所以AC=12.
AC×BE,即16×3=4×AC,所以AC=12.
由三角形面积公式可得S△ABC=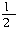 BC×AD=
BC×AD=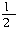 AB×CF,即16×3=6×AB.
AB×CF,即16×3=6×AB.
所以AB=8.
所以三角形ABC的周长为16+12+8=36.
41.解析:利用角平分线的性质解.
解:因为AI、BI、CI为三角形ABC的角平分线,
所以∠BAD=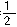 ∠BAC,∠ABI=
∠BAC,∠ABI=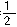 ∠ABC,∠HCI=
∠ABC,∠HCI=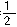 ∠ACB.
∠ACB.
所以∠BAD+∠ABI+∠HCI=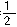 ∠BAC+
∠BAC+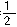 ∠ABC+
∠ABC+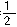 ∠ACB=
∠ACB=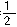 (∠BAC+∠ABC+∠ACB)=
(∠BAC+∠ABC+∠ACB)=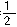 ×180°=90°.
×180°=90°.
所以∠BAD+∠ABI=90°-∠HCI.
又因为∠BAD+∠ABI=∠BID,90°-∠HCI=∠CIH,
所以∠BID=∠CIH.
所以∠BID和∠CIH是相等的关系.
40.解析:我们可以用字母代替甲、乙、丙、丁,用角度代表方向.把题中数据与图形一一对应,利用各方向的关系可求出丁岛分别在甲岛和乙岛的方向.
解:设甲岛处的位置为A,乙岛处的位置为B,丙岛处的位置为D,丁岛处的位置为C.如图:

因为丁岛在丙岛的正北方,
所以CD⊥AB.
因为甲岛在丁岛的南偏西52°方向,
所以∠ACD=52°.
所以∠CAD=180°-90°-52°=38°.
所以丁岛在甲岛的东偏北38°方向.
因为乙岛在丁岛的南偏东40°方向,
所以∠BCD=40°.
所以∠CBD=180°-90°-40°=50°.
所以丁岛在乙岛的西偏北50°方向.
39.解析:要想求∠EDF的度数,我们可以利用平角定义,只要能求出∠EDB即可.而∠EDB在三角形BDE中,只要能求出∠B就可以利用三角形内角和求∠EDB.而∠B又等于∠C,题中告诉了三角形DFC的一个外角∠AFD=140°,所以我们能得出∠C的度数.
解:因为∠AFD是三角形DCF的一个外角.
所以∠AFD=∠C+∠FDC.
即140°=∠C+90°.
解得∠C=50°.
所以∠B=∠C=50°.
所以∠EDB=180°-90°-50°=40°.
所以∠FDE=180°-90°-40°=50°.
38.A
(点拨:由∠1=∠2,知AD平分∠BAE,但AD不是三角形ABE内的线段,所以(1)不正确;同理,BE虽然经过三角形ABD边AD的中点G,但BE不是三角形ABD内的线段,故(2)不正确;由于CH⊥AD于H,故CH是三角形ACD边AD上的高,(3)正确.应选A.)
37.C
(点拨:因为EG⊥AD,交点为H,AD平分∠BAC,所以在直角三角形AHE中,∠1=90°-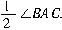 ,在三角形ABC中,易知∠BAC=180°-(∠2+∠3), 所以∠1=90°-
,在三角形ABC中,易知∠BAC=180°-(∠2+∠3), 所以∠1=90°-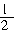 [180°-(∠2+∠3)]=
[180°-(∠2+∠3)]=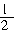 (∠3+∠2). 又因为∠1是三角形EBG的外角,所以∠1=∠2+∠G.
(∠3+∠2). 又因为∠1是三角形EBG的外角,所以∠1=∠2+∠G.
所以∠G=∠1-∠2=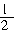 (∠3+∠2)-∠2=
(∠3+∠2)-∠2=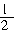 (∠3-∠2). )
(∠3-∠2). )
36.A
(点拨:由三角形的三边关系知:若长度分别为2cm、4cm、6cm,不可以组成三角形;若长度分别为4cm、6cm、8cm,则可以组成三角形;若长度分别为2cm、4cm、8cm,则不可以组成三角形;若长度分别为2cm、6cm、8cm,则不可以组成三角形.即分别为2cm、4cm、6cm、8cm的木棒,从中任取三根,能组成三角形的个数为1,故应选A.)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com