4. 牛刀小试

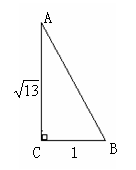根据下列图中所给条件分别求出下列图中∠A、∠B的正切值.

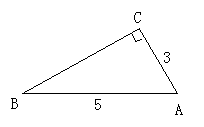
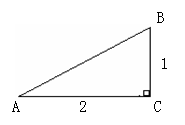
(通过上述计算，你有什么发现？_____________________________________.)

3. 正切的定义

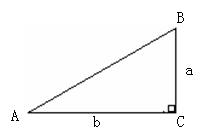
如图，在Rt△ABC中，∠C＝90°，a、b分别是∠A的对边和邻边.我们将∠A的对边a与邻边b的比叫做∠A_______，记作______.

即：tanA＝________＝__________

(你能写出∠B的正切表达式吗？)试试看.

2. 思考与探索二：

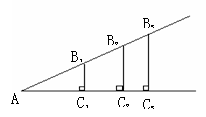
(1)如图，一般地，如果锐角A的大小已确定，我们可以作出无数个相似的RtAB₁C₁，RtAB₂C₂，RtAB₃C₃……，那么有：Rt△AB₁C₁∽________∽________……

根据相似三角形的性质，得：

＝_________＝_________＝……

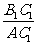(2)由上可知：如果直角三角形的一个锐角的大小已确定，那么这个锐角的对边与这个角的邻边的比值也_________.

1. 思考与探索一：

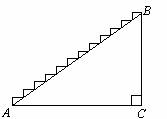
如何描述台阶的倾斜程度呢？

①　　 可通过测量BC与AC的长度，再算出它们的比，

来说明台阶的倾斜程度.

(思考：BC与AC长度的比与台阶的倾斜程度有何关系？)

答：_________________________________________.

②讨论：你还可以用其它什么方法？能说出你的理由吗？

答：_________________________________________.

2. 问题：下列图中的两个台阶哪个更陡？你是怎么判断的？

1. 观察：如图，是某体育馆，

为了方便不同需求的观众，

该体育馆设计了多种形式的台阶.

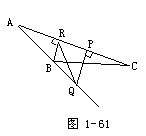
6．如图1－61所示．P是△ABC的AC边的中点，PQ⊥AC交AB延长线于Q，BR⊥AC于R．

　求证：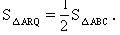

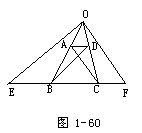
5．如图1－60所示．在梯形ABCD中，两腰BA，CD的延长线相交于O，OE∥DB，OF∥AC且分别交直线BC于E，F．求证：BE=CF．

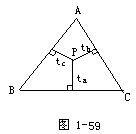
4．如图1－59所示．P为△ABC内任意一点，三边a，b，c的高分别为h_a，h_b，h_c，且P到a，b，c的距离分别为t_a，t_b，t_c．

　求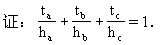

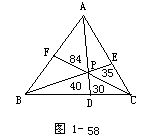
3．如图1－58所示．已知P为△ABC内一点，AP，BP，CP分别与对边交于D，E，F，把△ABC分成六个小三角形，其中四个小三角形的面积已在图中给出．求△ABC的面积．