
2.在日常生活中,观察各种建筑物的地板,你就能发现地板常用各种正多边形地砖铺砌成美丽的图案,也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下一丝空白,又不互相重叠(在几何里叫做平面镶嵌),这显然与正多边形的内角大小有关,当围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.
(1)如图1,请根据下列图形,填写表中空格:
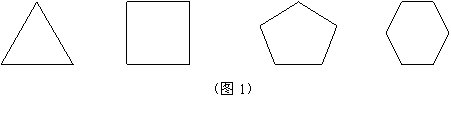
|
正多边形边数 |
3 |
4 |
5 |
6 |
… |
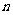 |
|
正多边形每个内角的度数 |
|
|
|
|
|
|
(2)如果限于一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形?
(3)从正三角形、正方形、正六边形中选一种,再在其它正多边形中选一种,请画出用这两种不同的正多边形镶嵌成一个平面图,并探索这两种正多边形共能镶嵌成几种不同的平面图形?说明你的理由.
A卷基础题答案
1.某同学在计算多边形的内角和时,得到的答案是1125°,老师指出他少加了一个内角的度数,你知道这个同学计算的是几边形的内角和吗?他少加的那个内角的度数是多少?
2.若一个正多边形的每一个外角都是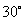 ,那么从某一个项点出发的所有对角线会将其分成_____个三角形
,那么从某一个项点出发的所有对角线会将其分成_____个三角形
3由于一个多边形的外角最多能有_____个钝角,因此,一个多边形的内角最多能有_____个锐角.
4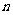 边形内角和与外角和的差为
边形内角和与外角和的差为 ,则
,则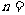 _____.
_____.
1.列举几个你所见到的能够密铺的“基本单位”:_____、_____、_____.(至少写出三种)
1如果一个多边形的每个外角,都是与它相邻内角的三分之一,则这样的多边形有( )
A.无穷多个,它的边数为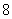 B.一个,它的边数为
B.一个,它的边数为
C.无穷多个,它的边数为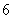 D.无穷多个,它的边数不可能确定
D.无穷多个,它的边数不可能确定
 2如图,若
2如图,若 ,那么
,那么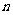 等于( )
等于( )
A.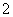 B.
B.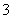 C.
C.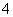 D.
D.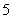
3一个多边形恰有三个内角是钝角,那么这个多边形的边数最多为( )
A.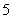 B.
B.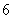 C.
C.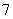 D.
D.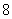
4.(本题12分)几边形的内角和是2160°?是否存在一个多边形的内角和为1000°?
B卷提升题
3.(本题12分)一个多边形除了一个内角之外,其余内角之和为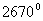 ,求这个内角的大小.
,求这个内角的大小.
2.(本题10分)如果一个凸多边形的所有内角从小到大排列起来,恰好依次增加的度数相同,设最小角为100°,最大角为140°,那么这个多边形的边数为多少?
1.(本题10分)一个四边形的内角的度数的比是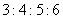 ,求它的最大内角和最小外角的度数.
,求它的最大内角和最小外角的度数.
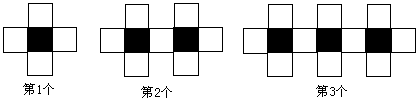
8.黑白两种颜色的正方形纸片,按如图所示的规律拼成若干个图案,(1)第4个图案中有白色纸片_____块。(2)第n个图案中有白色纸片_____块。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com