5.如图所示，AB∥CD，AD，BC交于O，∠A=35°，∠BOD=76°，则∠C的度数是(　　 )

A.31°　　　 B.35°　　 C.41°　　 D.76°

4.如图所示，∠1+∠2+∠3+∠4的度数为(　　　　 )

A100°　　　　　　　　 B.180°　　 C.360°　　　　　　　 D.无法确定

3.一个三角形的内角中，至少有(　　　 )

A一个内角　　　 B.两个内角　　 C.一内钝角　　　　 D.一个直角

2.在△ABC中，若∠A=∠B=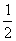∠C，则∠C等于(　　　　 )

A.45°　　 B.60°　　 C.90°　　　 D.120°

1.在我们的生活中处处有数学的身影，请看图，折叠一张三角形纸片，

把三角形的三个角拼在一起，就得到一个著名的几何定理，请你写

出这一定理的结论：三角形的三个内角和等于　　　　　　 °

2．(1)60°，90°，108°，120°，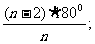

(2)正三角形、正方形、正六边形；

(3)答案不唯一，如正方形和正八边形，正三角形和正十二边形．

下边以正方形和正八边形为例说明．图略，

设在一个顶点周围有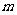个正方形的角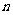，个正八边形的角，那么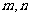应是方程的整数解，即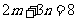的整数解，而这个方程的整数解只有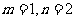这一组，所以符合条件的图形只有一种．

4．解: 设该多边形为n边形，依题意得

　 (n－2)·180°=2160°

　 ∴ n =14

不存在这样的多边形，理由如下:

假设存在这样的n边形，依题意得

(n－2)·180°=1000°

∴ n=

∵ 多边形的边数为正整数

∴不存在这样的多边形．

B卷提升题答案

3．．

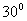2．依题意可知多边形的内角平均度数为120°．

设多边形的边数为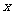，则有12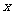0=()180，

解得．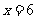

故此多边形为六边形．

3．　6.15　 16、13，3n+1