1.根据图形填空：

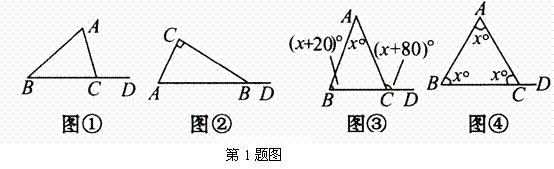
(1)如图①，已知∠A=72°，∠B=38°，则∠ACD=　　　　 .；

(2)如图②已知AC⊥BC∠CBD=148°，则∠A=　　　　 ；

(3)如图③，=　　　　 ；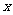

(4)如图④∠A =∠B=∠C=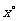，则∠ACD=　　　　 .；

9.解：∵∠B=50°，∠C=70°，

∴∠BAC=60°，又∵AD是△ABC的角平分线

∴∠BAD=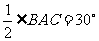.又∵AE是△ABC的高　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

∴∠BAE=180°-∠B-∠AEB=40°，∴∠DAC=∠BAE-∠BAD=10°.

第二课时7.2.2三角形的外角

7.300°，提示：∵∠1+∠2=180°-30°=150°，∠3+∠4=180°-30°=150°，

∴∠1+∠2+∠3+∠4=150°+150°=300°；8.A

6.(1)40°；(2)65°；(3)30°，60°，90°(4)30°

5.C，提示：∵AB∥CD，∴∠D=∠A=35°. ∠DOC=180°-∠BOD=180°-76°=104°，

在△COD中，∠C=180°-∠D-∠DOC=180°-35°-104°=41°；

1.180；2.C，提示：依据三角形内角和定理得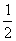，∠C+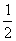∠C+∠C=180°，解得∠C=90°；3.B；4.C，提示：作如图辅助线，这样把∠1、∠2、∠3、

∠4四个角的和转化为两个三角形的内角和，

即2×180°=360°

9.如图所示，AD、AE分别是△ABC的角平分线和高，若∠B=50°，∠C=70°，

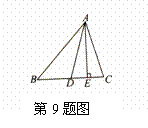求∠DAC的度数.

第一课时答案：

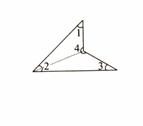
8.一幅三角板，如图所示叠放在一起，则 2中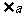的度数为(　　　 )

A.75°　　 B.60°　　 C.65°　　 D.55°

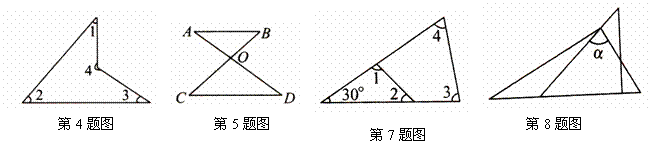
7.如图所示，∠1+∠2+∠3+∠4的度数为　　　　　　 .

6.在△ABC中：(1)若∠A=80°，∠B=60°，则∠C=　　　　 　

(2)若∠A=50°，∠B=∠C，则∠C=　　　　

(3)若∠A∶∠B∶∠C=1∶2∶3，则∠A=　　　　 ∠B=　　　　 ∠C=　　　　 ；

(4)若∠A=80°，∠B-∠C=40°，则∠C=