
6.如果两条直线被第三条直线所截,那么一组内错角的平分线( )
A.互相垂直; B.互相平行; C.互相重合; D.以上均不正确.
5.用A、B、C分别表示学校、小明家、小红家,已知学校在小明家的南偏东25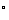 ,小红家在小明家正东,小红家在学校北偏东35
,小红家在小明家正东,小红家在学校北偏东35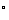 ,则∠BAC=( )
,则∠BAC=( )
A.35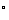 ;
B.55
;
B.55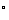 ;
C.60
;
C.60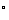 ;
D.65
;
D.65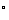 .
.
4.如图,直线c与直线a、b相交,且a//b,则下列结论:(1) ;(2)
;(2)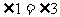 ;(3)
;(3)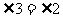 中正确的个数为( )
中正确的个数为( )
A.0; B.1; C.2; D.3.
3.一架飞机向北飞行,两次改变方向后,前进的方向与原来的航行方向平行,已知第一次向左拐50°,那么第二次向右拐( )
A.40°; B.50°; C.130°; D.150°.
2.如图,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE=
125°,则∠DBC的度数为( )
A.55°; B.65°; C.75°; D.125°.
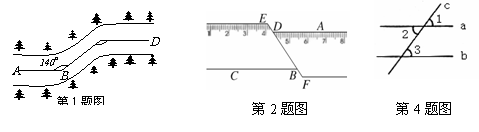
1.一条公路两次转弯后又回到原来的方向(即AB∥CD,如图4.1-15),如果第一次转弯时的∠B=140°,那么,∠C应是( )
A.40°; B.100°; C.140°; D.180°.
5. 通过交流,培养学生之间的团结协作能力,让学生用自己的语言清楚的表达解决问题的过程,提高语言表达能力。
4. 通过改变题目的条件,让学生再一次经历猜想、论证这一思维过程,加深对所学知识的理解及灵活运用能力。在探索中再一次发展学生的分析问题、解决问题的能力和推理能力。
3. 在思考证明途径过程中通过一题多解,既能让学生在一连串的变化中熟练使用三角形内角和定理及外角性质,同时也让学生体验数学活动充满探索,体验解决问题策略的多样性。通过观察──猜想──论证这一数学活动过程,让学生感受由特殊到一般的数学推理过程和数学思考方法。
2. 让学生动手作图、测量一系列的活动,既能让学生自我猜想,获取知识,又能为证明的思路提供启发。培养了学生在几何方面的动手、动脑能力;和“由特殊到一般”这一探索问题的能力,开拓学生的思维。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com