1、在Rt△ABC中，∠C＝90°，分别写出∠A的三角函数关系式：sinA＝_____，cosA=_____，tanA＝_____.∠B的三角函数关系式_________________________.

已知在△ABC中，a、b、c分别为∠A、∠B、∠C的对边，且a：b：c＝5：12：13，试求最小角的三角函数值.

3、如图，在Rt△ABC中，∠C＝90°，

BC＝9a，AC＝12a，AB＝15a，tanB=________,

cosB=______,sinB=_______

2、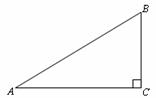在Rt△ABC中，∠C＝90°，AC＝1，BC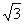＝，则sinA＝_____，cosB=_______,cosA=________,sinB=_______.

1、如图，在Rt△ABC中，∠C＝90°，

AC＝12，BC＝5，则sinA＝_____，

cosA＝_____，sinB＝_____，cosB＝_____.

6、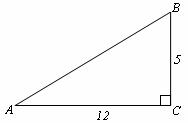锐角A的正弦、余弦和正切都是∠A的__________.

0.26个单位长度，在水平方向前进了约0.97个单位长度.

根据正弦、余弦的定义，可以知道：

sin15°＝0.26，cos15°＝0.97

(2)你能根据图形求出sin30°、cos30°吗？

sin75°、cos75°呢？

sin30°＝_____，cos30°＝_____.

sin75°＝_____，cos75°＝_____.

(3)利用计算器我们可以更快、更精确地求得各个锐角的正弦值和余弦值.

(4)观察与思考：

从sin15°，sin30°，sin75°的值，你们得到什么结论？

____________________________________________________________.

从cos15°，cos30°，cos75°的值，你们得到什么结论？

____________________________________________________________.

当锐角α越来越大时，它的正弦值是怎样变化的？余弦值又是怎样变化的？

____________________________________________________________.

5、思考与探索

怎样计算任意一个锐角的正弦值和余弦值呢？

(1)　　　 如图，当小明沿着15°的斜坡行走了1个单位长度时，他的位置升高了约

4、牛刀小试

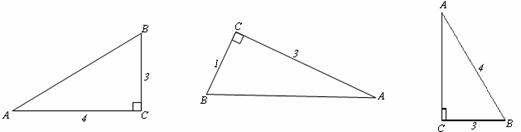根据如图中条件，分别求出下列直角三角形中锐角的正弦、余弦值.

3、余弦的定义

如图，在Rt△ABC中，∠C＝90°,

我们把锐角∠A的邻边b与斜边c的比叫做∠A的______，记作=_________，

即：cosA=______=_____.

(你能写出∠B的正弦、余弦的表达式吗？)试试看.

___________________________________________________.