1.　　 一个三角形中，至少有＿个锐角，至多有___个直角，最多有___个钝角.

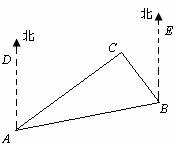
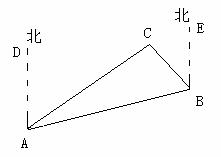
2.　　 如图，C岛在A岛的北偏东50°方向，B岛在A岛的北偏东80°方向，C岛在B岛的北偏西40°方向.从C岛看A、B两岛的视角∠ACB是多少度？

活动3　课堂小结

这节课我的收获是：

活动4　课堂练习

1.　　 ⑴△ABC中，∠A＝35°，∠B＝65°，则∠C＝______.

⑵　　 △ABC中，∠A＝120°，∠B＝2∠C，则∠C＝______.

⑶　　 △ABC中，∠A +∠B＝∠C，则∠C＝______.

⑷　　 △ABC中，∠C＝90°，∠B＝28°，则∠A＝______.

归纳：三角形内角和定理，揭示了三角形三个内角之间的关系，运用它可以解决：

在三角形中，已知两角可求第三角，或已知各角之间的关系求各角；

在直角三角形中，已知一个锐角，可以求另一个锐角.

2.　　　 解决问题

动手操作　在纸上画一个三角形，并将它的内角剪下拼合在一起，就得到一个_____.

⑴

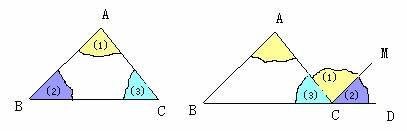
⑵

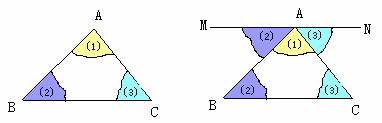
上面的拼合中，有不同的方法.你用了哪种方法？从这个操作过程中，你能发现证明的思路吗？小组讨论、交流展示.

于是就证明了三角形内角和定理　三角形三个内角的和等于_______.

活动2　简单应用

1.　　　 问题：

我们知道，任意一个三角形的三个内角的和等于180°.怎样证明这个结论呢？

通过度量的方法，可以验证一些具体的三角形的内角和等于180°，由于形状不同的三角形有无数个，我们不可能用度量的方法一一验证所有的三角形.

　于是，我们需要寻找一种能证明任意一个三角形的内角和等于180°的方法.

3.体会转化的数学思想方法.初步体会证明的思路方法

重点：三角形内角和定理

活动1　探究证明“任意一个三角形的三个内角的和等于180°”.

7.2.1三角形的内角　学案

学习目标　

1 经历实验活动的过程，得出三角形的内角和定理，能用平行线的性质推出这一定理

2 能应用三角形内角和定理解决一些简单的实际问题

练习：课本P80，练习1，2

作业：P81

1，2，3，4，5

补充练习

1 三角形中最大的角是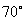，那么这个三角形是锐角三角形(　　 )

2 一个三角形中最多只有一个钝角或直角(　　　　 )

3 一个等腰三角形一定是锐角三角形(　　 )

4 一个三角形最少有一个角不大于(　　　 )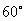

1在所准备的三角形硬纸片上标出三个内角的编码

2 让学生动手把一个三角形的两个角剪下拼在第三个角的顶点处，用量角器量出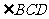的度数，可得到

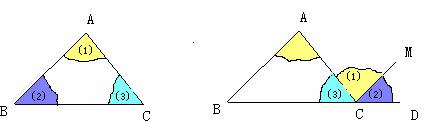
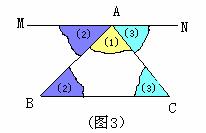
3 剪下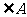，按图(2)拼在一起，从而还可得到

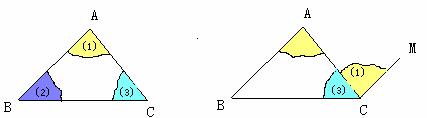
　　　　　　　 图2

4 把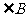和剪下按图(3)拼在一起，用量角器量一量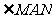的度数，会得到什么结果。

二想一想

如果我们不用剪、拼办法，可不可以用推理论证的方法来说明上面的结论的正确性呢？

已知，说明，你有几种方法？结合图(1)、图(2)、图(3)

能不能用图(4)也可以说明这个结论成立

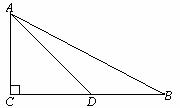
5、在△ABC中，∠C＝90°，D是BC的中点，且∠ADC＝50°，AD＝2，求tanB的值.(精确到0.01m)(参考数据：sin50°≈0.7660，cos50°≈0.6428，tan50°≈1.1918)