
3、试一试:你认为什么是平移?
(1)定义:在平面内,将一个图形沿着某个方向移动一定的距离,叫做图形的平移.
(2)平移的补充定义:平移不改变图形的形状、大小,改变了图形的位置.
2、“做一做2”:
 (1)议一议:p.17的“做一做”中第2题(前后四人为学习小组,共同合作完成)
(1)议一议:p.17的“做一做”中第2题(前后四人为学习小组,共同合作完成)
(2)说一说:
(a)生:变化规律--每一行的第一个三角形,不断向右平移3格得到的这一行.
(b)课件动画演示:每一行的第一个三角形,不断向右平移3格得到原图
(c)实物投影展示:同学们的书本,图8-16的全图
(d)课件显示:图8-16,经平移得到全图

(f)图中,三角形沿着某个一方向(向右)平行移动了一段距离(3格),所得图形(三角形)与原图形(三角形)比较,形状、大小没有发生变化,只是位置发生了改变.
1、“做一做1”:
(1)动一动:(a)在桌面上将手中的三角板沿刻度尺向右平移2cm
(b) 在桌面上将手中的三角板沿刻度尺向左平移3cm.
(2)议一议:p.16的“做一做”中第1题(前后四人为学习小组,共同合作完成)
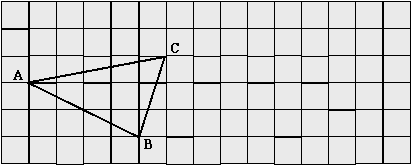
(3)说一说:
(a)实物投影仪展示:学生书本所画图形.
(b)生:画法--……;度量得--AB=A′B′……;
发现--移动前后,三角形的三条边的大小,没有发生变化.三个角的大小……;三角形的形状、大小,没有发生变化.
(e)课件动画演示:((a))点A向右移动6格,得点A′;点B……;点C……;连结A′B′…….
((b))△ABC向右移动6格,与△A′B′C′重合.
(f)图中,△ABC沿着某个一方向(向右)平行移动了一段距离(6格),所得图形(△A′B′C′)与原图形(△ABC)比较,形状、大小没有发生变化,只是位置发生了改变.
3、引入课题:
在上述平移运动中,我们发现都有一个共同点,这些物体都是沿着某一方向作平行移动.
生活中有许多平移的现象,如果我们让简单的图形也平移起来,展现的又会是怎样的一番风景呢--课题:图形的平移.
2、看一看:
刚才的大楼被平移了,我们接着再来看一组镜头.
一组镜头:开关抽屉、推开铝合金窗、推拉木门、自动门开关、乘坐手扶电梯.
1、听一听:向学生介绍江南大酒店被整体平移的事情,引入平移的话题.
(备注1:渗透爱国主义教育,贴近江苏本地生活.备注2:这个例子渗透了平移定义.)
(四)总结、扩展
底数是相反数的幂相乘时,应先化为同底数幂的形式,再用同底数幂的乘法法则,转化时要注意符号问题.
(三)教学过程
1.创设情境、复习导入
(1)叙述同底数幂乘法法则并用字母表示.
(2)指出下列运算的错误,并说出正确结果.
①
②
③
强调:①中 的指数不为0,指数相加时不要漏加
的指数不为0,指数相加时不要漏加 的指数.②不是同类项不能合并.③同底数幂相乘,指数相加不是相乘.
的指数.②不是同类项不能合并.③同底数幂相乘,指数相加不是相乘.
(3)填空:
① ,
,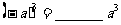
② ,
, ,
,

2.探索新知,讲授新课
例1 计算:
(1)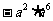 (2)
(2)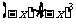 (3)
(3)
解:(1)原式
(2)原式
(3)原式
例2 计算:
(1) (2)
(2)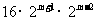
(3)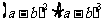 (4)
(4)
解:(1)原式
(2)原式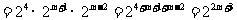
(3)原式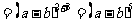
(4)
或原式
提问: 和
和 相等吗?
相等吗?
3.巩固熟练
(1)P93 练习(下)1,2.
(2)计算:
①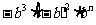 ②
②
③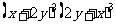 ④
④
(3)错误辨析:
计算:①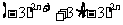 (
( 是正整数)
是正整数)
解:
说明: 化简错了,
化简错了, 是正整数,
是正整数,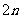 是偶数,据乘方的符号法则
是偶数,据乘方的符号法则 本题结果应为0.
本题结果应为0.
②
解:原式
说明: 与
与 不是同底数幂,它们相乘不能用同底数幂的乘法法则,正确结果应为
不是同底数幂,它们相乘不能用同底数幂的乘法法则,正确结果应为
(二)整体感知
要准确掌握同底数幂的乘法法则,并会运用它熟练灵活地进行同底数幂的乘法运算,对于运算法则,我们除了应掌握它们的正用: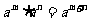 外,还要善于根据题目的结构特征,学会它们的逆向应用:
外,还要善于根据题目的结构特征,学会它们的逆向应用: ,当然这个难度较大.在应用同底数幂乘法法则计算时,要注意防止把幂的乘法运算性质与整式加法相混淆.乘法只要求同底就可以用性质计算,而加法则不仅要求底数相同,而且指数也必须相同.
,当然这个难度较大.在应用同底数幂乘法法则计算时,要注意防止把幂的乘法运算性质与整式加法相混淆.乘法只要求同底就可以用性质计算,而加法则不仅要求底数相同,而且指数也必须相同.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com