
4.从n边形一个顶点出发,可以引出(n一2)条对角线,得到(n一2)个三角形.( )
3.三角形的外角和与一多边形的外角和相等.( )
2.当多边形边数增加时.它的外角和也随着增加.( )
1.当多边形边数增加时,它的内角和也随着增加.( )
课本P90第4、5、6题.
备选题:

引导学生总结本节课主要内容.
课本P89练习1、2、3题.
P90第2、3题
例1 如果一个四边形的一组对角互补,那么另一组对角有什么关系?
已知:四边形ABCD的∠A+∠C=180°.求:∠B与∠D的关系.
分析:本题要求∠B与∠D的关系,由于已知∠A+∠C=180°,所以可以从四边形的内角和入手,就可得到完满的答案.
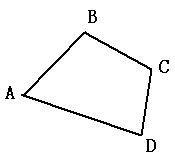
解:如图,四边形ABCD中,∠A+∠C=180°。
∵∠A+∠B+∠C+∠D=(4-2)×360°=180°,
∴∠B+∠D= 360°-(∠A+∠C)=180°
这就是说:如果四边形一组对角互补,那么另一组对角也互补.
例2 如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等于多少?
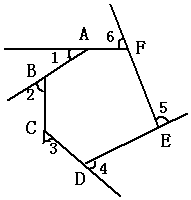
已知:∠1,∠2,∠3,∠4,∠5,∠6分别为六边形ABCDEF的外角.
求:∠1+∠2+∠3+∠4+∠5+∠6的值.
分析:关于外角问题我们马上就会联想到平角,这样我们就得到六边形的6个外角加上它相邻的内角的总和为6×180°.由于六边形的内角和为(6-2)×180°=720°.
这样就可求得∠1+∠2+∠3+∠4+∠5+∠6=360°.
解:∵六边形的任何一个外角加上它相邻的内角和为180°.
∴六边形的六个外角加上各自相邻内角的总和为6×180°.
由于六边形的内角和为(6-2)×180°=720°
∴它的外角和为6×180°一720°=360°
如果把六边形横成n边形.(n为不小于3的正整数)
同样也可以得到其外角和等于360°.即
多边形的外角和等于360°.
所以我们说多边形的外角和与它的边数无关.
对此,我们也可以象以下这种,理解为什么多边形的外角和等于360°.
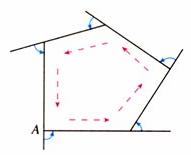
如下图,从多边形的一个顶点A出发,沿多边形各边走过各顶点,再回到A点,然后转向出发时的方向,在行程中所转的各个角的和就是多边形的外角和,由于走了一周,所得的各个角的和等于一个周角,所以多边形的外角和等于360°.
3.从n边形的一个顶点出发,可以引几条对角线?它们将n边形分成几个三角形?n边形的内角和等于多少度?
综上所述,你能得到多边形内角和公式吗?
设多边形的边数为n,则
n边形的内角和等于(n一2)·180°.
想一想:要得到多边形的内角和必需通过“三角形的内角和定理”来完成,就是把一个多边形分成几个三角形.除利用对角线把多边形分成几个三角形外,还有其他的分法吗?你会用新的分法得到n边形的内角和公式吗?
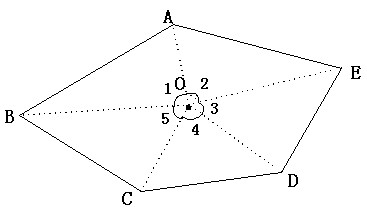
由同学动手并推导在与同伴交流后,老师归纳:(以五边形为例)
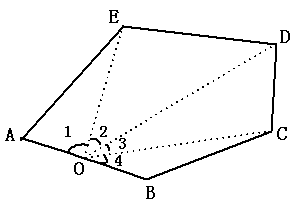
分法一:在五边形ABCDE内任取一点O,连结OA、OB、OC、OD、OE,则得五个三角形.其五个三角形内角和为5×180°,而∠1,∠2,∠3,∠4,∠5不是五边形的内角应减去,∴五边形的内角和为5×180°一2×180°=(5-2)×180°=540°.
如果五边形变成n边形,用同样方法也可以得到n个三角形的内角和减去一个周角,即可得:n边形内角和=n×l80°一2×180°=(n一2)×180°.
分法二:在边AB上取一点O,连OE、OD、OC,则可以(5-1)个三角形,而∠1、∠2、∠3、∠4不是五边形的内角,应舍去.
∴五边形的内角和为(5-1)×180°一180°=(5-2)×180°
用同样的办法,也可以把n边形分成(n一1)个三角形,把不是n边形内角的∠AOB舍去,即可得n边形的内角和为(n一2)×180°.
2.从五边形一个顶点出发可以引几条对角线?它们将五边形分成几个三角形?那么这五边形的内角和为多少度?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com