
在教学中采用的教学流程,使学生对多边形的内角和经过引入──掌握──熟练──提高的过程,既掌握知识,又提高能力,培养兴趣。
2、通过将多边形问题转化为三角形问题解决,使学生体会化归思想的应用方法,从而提高分析问题和解决问题的能力。
[情感目标]
通过三角形和多边形之间的联系与区别的分析研究,培养学生辩证唯物主义观点和激发学生学习几何的兴趣。
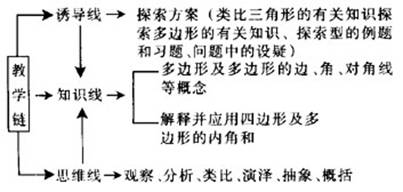
其中,以知识目标为主线,能力、情感目标渗透于知识目标中来体现。确定此目标基于以下几点:新课程标准要求、教材编写意图,七年级学生实际、素质教育需要、布卢姆目标分类理论等。为完成教学目标,设计知识线、诱导线、思维线三线合一的教学链。
点评 三维立体目标,体现了数学的技术教育功能和文化教育功能。素质教育的重点是培养学生的创新精神和实践能力,将素质教育的重点落实在教学目标中,是教师对数学教育有深人理解的体现。
教学重点、难点:
“多边形”在教材中起着承上启下的作用,它既是前面所学的“三角形”知识的应用,也是后面学习用正多边形拼地板、各种特殊四边形的重要的预备知识。因此,本节课的教学重点是:多边形内角和。另外培养学生主动探究新知识的方法也是本节课的一个重点。三角形的三个顶点确定一个平面,所以三个顶点总是共面的。但四边形的四个顶点有不共面的情况,又限于我们现在研究的是平面图形,所以在四边形定义中有“在平面内”这个条件,学生对这一条件的理解是难点。
突出重点、化解难点的措施是:(l)教师自制教具,操作演示;(2)随时总结学习几何命题的一些规律,在得出结论前“引导分析”;(3)本节课内容较多,但各部分知识之间的联系密切,为了便于学生学习,教学中既注重各部分知识之间的联系,又注意保持各部分知识之间相对的独立性。使其条理清楚,层次分明;(4)利用表格使所学知识形成网络;(5)设计有目的、有梯度、循序渐进的练习题组,强化训练。
1、通过多边形定义及内角和学习,增强类化推理和发散思维能力。
2、解释并会验证四边形内角和、n边形的内角和,会应用它进行简单的计算和说理。
[能力目标]
[认知目标]
1、知道四边形、多边形、正多边形的定义,能够在图形中识别它们的有关概念。
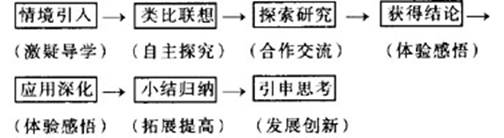
3、多边形内角和公式导出后,安排“算一算”这一教学环节,一方面是应用新知识,另一方面试图从四边形的外角和着手来推出一个不变的规律:多边形的外角和都等于360度,让学生体会从特殊到一般、不完全归纳法等重要的数学思想方法。
2、在探求多边形的内角和中,以学生极为熟悉的四边形开始研究,通过学生思考、相互交流,师生及时共同归纳出探求多边形内角和的基本思路,在适时地引导学生思维方向的同时,达到本节教学的基本目标
1、在引入新课时,借助四个全等的四边形教具的演示实验以及数学基础知识抢答赛,模拟了较为真实的情境来引题开展教学,让学生能及时有效地集中注意力,对本节内容产生疑问与好奇心.
2、选做题:教科书90页习题7.3第6、7、8题;教科书96页复习题第5、6、7、8题。
[教学反思]
1、必做题:教科书90页习题7.3第2、、3、4、5题;教科书96页复习题第7题第2、3题。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com