2.下列说法中，错误的是……………………………………………………………(　　 )

　 A.一个三角形的三个内角中，至少有一个角不大于60⁰

B.有一个外角是锐角的三角形是钝角三角形

C.锐角三角形中，两个角的和小于直角

D.直角三角形中有一个外角等于和它相邻的内角

1.若一个三角形的三个内角不相等，则它的最小角不能大于……………………(　　 )

　 A.45⁰　　　　　　 B.60⁰　　　　　 C.90⁰　　　　　 D.120⁰

5. 点D在BC的延长线上，DE⊥AB于E,交AC于F, ∠B=50⁰, ∠CFD=60⁰

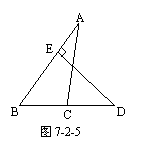
则∠ACB=

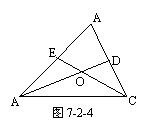
4.如图7-2-4，BD、CE是△ABC的角平分线，交于点O,若∠BOC=138⁰,则∠A=

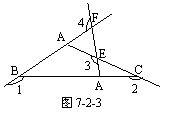
3.如图7-2-3，∠1+∠2+∠3+∠4=

2.在△ABC中，若∠A-∠B=20⁰, ∠A=2∠C,则∠A=　　　　 .∠B　　 .∠C=　　　 .

1.一个三角形的两个内角分别为50⁰和61⁰，则第三个内角为　　　　 .

7.2　　 与三角形有关的角

　　 通过上一节课的学习，你对三角形已经有了足够的认识了吧，我们知道，三角形除了变以外还有角，那么你想知道三角形的角分为那两类吗？三角形的角又有怎样的性质呢？通过本节的学习你就知道谜底啦！

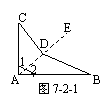
　 [例1]一个零件的形状如图7-2-1所示，按规定，∠BAC=90⁰, ∠B=21⁰,∠C=20⁰,检验工人量得∠BDC=130⁰,就断定这个零件不合格，运用所学知识说明不合格的理由.

[点拨]把实际问题转化为三角形的知识来解，关键是通过转化建立起数学模型.

[答案]依据三角形内角和定理的推论，连结AD并延长到点E，则

∠CDE=∠C+∠1, ∠BDE=∠B+∠2,∴∠CDE+∠BDE=∠C+∠1+∠B∠2,

即∠CDB =∠C+∠B+∠CAB.若零件和格，则有∠BDC=90⁰+20⁰+21⁰=131⁰,

而量得∠CDB=130⁰, ∴零件不合格.

[例2](1)如图7-2-2(1),在△ABC中，∠C>∠B,AD⊥BC于D,AE平分∠BAC,

则∠EAD与∠B, ∠C有和数量关系？

(2)如图7-2-2(2),AE平分∠BAC,F为其上一点,FD⊥BC于D,这时∠EFD与∠B、∠C又有何数量关系？

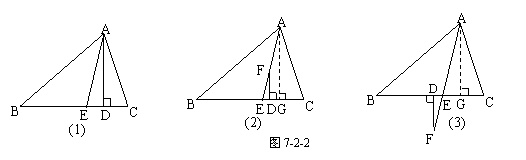(3) 如图7-2-2(3),AE平分∠BAC,F为AE的延长线上的一点，FD⊥BC于D,这时∠AFD与∠B、∠C又有何数量关系？

[点拨]在处理三角形中的角的问题时，又是需要从整体出发进行考虑，有时也可以通过适当添加辅助线使未知问题转化为已经解决的问题.本题中第(1)问要找出∠EAD与∠B、∠C的数量关系，可以考虑利用三角形内角和等于180⁰及三角形外角性质.为此，把∠EAD、∠B、∠C先放到具体的三角形中，∠EAD可看作△ADE的一个内角，也可看作∠EAC与∠DAC的差或∠BAD与∠BAE的差.

本题第(2)、(3)小题，可先作出BC边上的高，得到∠EAC,再确定∠EFD(如图7-2-2(2)、图7-2-2(3).

[答案](1)∵AE平分∠BAC　 ∴∠BAE=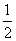∠BAC　 ∵∠BAC=180⁰-∠B-∠C

∴∠BAE=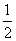(180⁰-∠B-∠C)=90⁰-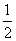∠B-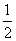∠C　 ∵∠AED=∠B+∠BAE

∴∠AED=180⁰-∠AED-∠ADB　 ∠EAD=180⁰-(90⁰+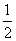∠B-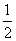∠C)-90⁰

=180⁰-90⁰-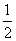∠B+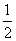∠C-90⁰=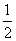(∠C-∠B)

(2)如图7-2-2(2)，过A作AG⊥BC于G,由(1)知，∠EAG=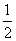(∠C-∠B) ∵AG⊥BC

∴∠AGC=90⁰ ∵FD⊥BC　 ∴∠FDG=90⁰　 ∴∠AGC=∠FDG　 ∴FD//AG ∴∠EFD=∠EAG

∴∠EFD=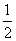(∠C-∠B)

(3) 如图7-2-2(3)，过A作AG⊥BC于G,由(1)知，∠EAG=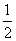(∠C-∠B) ∵AG⊥BC

∠AGB=90⁰　 ∵FD⊥BC 　∴∠FDC=90⁰ ∴∠AGC=∠FDC　 ∴FD//AG ∴∠AFD=∠EAG

∴∠AFD=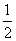(∠C-∠B)

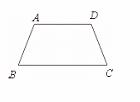
8．如图，已知：四边形ABCD中，∠A＝∠D，∠B＝∠C．求证：AD∥BC．

7．有两个多边形，如果它们都是各边相等，各内角相等的多边形，且这两个多边形的边数之比为1∶2．内角之比是3∶4，则这两个多边形的边数各是多少？