9、根据不等式的性质将下列不等式化为x＜a或x＞a的形式：

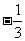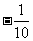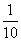(1)2x＜x－5 (2)x+1＜4 (3)x＜(4)＞

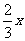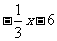
8、若a-b>a,a+b<b则有(　　 )

(A)ab<0　　 (B)>0　　 (C)a+b>0　　 (D)a-b<0

7、如图2，天平右盘中的每个砝码的质量都是1g，则物体A的质量m(g)的取值范围，在数轴上可表示为(　　 )

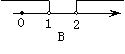
6、若a＞b,c＜0, 用“>”或“<”号填空．

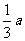
(1)　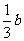　 　　(2)2a-4　　 2b-4 　 (3)-a　　 -b

(4)a+2　　 b+2 　 (5)ac²　　　 bc² 　　(6)ac　　 bc

(7)ac+c　　 bc+c 　(8)ac²+1　　 bc²+1

5、用不等号填空，并说明是根据不等式的哪一条性质：

若x+2＞5,则x　　　 3，根据　　　　　　　　　　 ；

若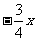＜－1，则x　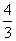　　 ，根据　　　　　　　　　　 ；

若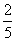x＜－3，则x　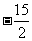　　 ，根据　　　　　　　　　　 ；

4、若，则下列各式中一定正确的是(　 )

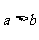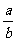A．　　　 B．　　 C．>0　　 D．

3、已知关于x的不等式(1－a)x＞2的解集是x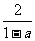＜，则a的取值范围(　　　 )

A、a＞0　 　B、a＞1　 C、a＜0　D、a＜1

2、若x＞y，则ax＞ay.那么一定有(　)

A、a＞0　　　　　 B、a≥0　　　　 C、a＜0　　　　　 D、a≤0

1、已知a＜b，下列式子中，错误的是(　)

A、4a＜4b　　 B、－4a＜－4b　　 C.、a+4＜b+4　 D、a－4＜b－4

3、不等式的基本性质3　 如果a>b，并且c<0，那么ac　　 bc，　 。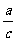

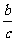不等式两边都乘以(或除以)同一个　　　 ，不等号的方向　　　　　 。

答： <、<、负数、改变

[范例点睛]

例1　 用“>”或“<”填空：

(1)a+3_____b+3；(a<b)；　　 (2)2a_____2b；(a>b)；

(3)(a>b)；　 　　(4)a－4_____b－4 (a－b>0) ；

(5)若a>0，b>0，则ab_____0； (6)若b<0，则a+b______a；

(7)当a<0时，b_____0时，ab>0．

思路点拨：含有几个字母的不等式(如ab<0)，先确定字母的取值，再根据不等式的性质判定不等号是否改变．

(1)由a<b，要得到a+3_____b+3，需要把不等式两边都加3，由不等式基本性质1可得；

(2)由a>b，要得到2a_____2b，需要把不等式两边都乘以2，由不等式基本性质2可得；

(3)由a>b，要得到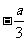　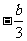　 ，需要把不等式两边都乘以，而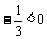，由不等式基本性质3可得；

(4)因为a-b>0，所以a>b，要得到a－4_____b－4，需要把不等式两边都减去4，由不等式基本性质1可得；

(5)把b看成正数，由不等式a>0得到ab　　 0，由不等式基本性质2可得；

(6)对不等式b<0，要得到a+b______a，需要把不等式两边加上a，由不等式基本性质1可得；

(7)对不等式a>0，两边乘以b后改变不等号的方向，由不等式基本性质3可得．

易错辨析：在应用不等式性质3时，要注意改变不等号的方向。

方法点评：灵活运用不等式的性质，它是解不等式的基础。

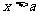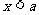例2 根据不等式的性质，把下列不等式化为或的形式：

(1)x+3<－2；(2)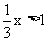；(3)7x>6x－4；(4)－x<0；　

思路点拨：未知数x的系数为1，次数为1，放在不等号的左边，常数移到不等号的右边。

易错辨析：特别注意(4)中不等式的两边同乘以一个负数，不等号的方向要改变．

方法点评：这里的变形，与方程变形中的移项相类似，将不等式一边的某一项改变符号后移到另一边去．变形与方程式中“将未知的系数化为1”相类似,但乘(除)一个负数，原不等号的方向要改变．将不等式化为x>a或x<a的形式，实际上就是求出了未知数取值的范围，即求出了所给不等式的解集．

例3 试判断下列各对整式的大小：

(1)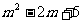和－2m+5；

(2)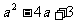和－4a+1．

思路点拨：根据不等式的性质1，我们可以得到另一种比较两个数(或代数式)的大小的方法：若A－B>0，则A>B；若A－B=0，则A=B；若A－B<0，则A<B．

方法点评：这种比较大小的方法，称为“作差比较法”，简称“比差法”．

当A，B两数都大于零时，还可用“比商法”比较两个正数A、B的大小：

若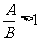，则A>B；若，则A=B；若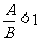，则A<B．

[课外链接]数学游戏：

有位老师，想辨别他的3个学生谁更聪明．他采用如下的方法：事先准备好3顶白帽子，2顶黑帽子，让他们看到，然后，叫他们闭上眼睛，分别给戴上帽子，藏起剩下的2顶帽子，最后，叫他们睁开眼，看着别人的帽子，说出自己所戴帽子的颜色． 3个学生互相看了看，都踌躇了一会，并异口同声地说出自己戴的是白帽子． 聪明的小读者，想想看，他们是怎么知道帽子颜色的呢？

[随堂演练]