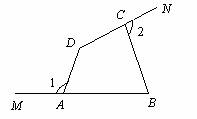
6.如图，∠1，∠2是四边形ABCD的外角，求证：∠1+∠2＝∠ADC+∠ABC.

5. 四边形的∠A、∠B、∠C、∠D的外角之比为1：2：3：4，那么∠A：∠B：∠C：∠D=　　　 ．

4.内角和等于外角和的多边形是　　　 边形．

3.多边形的每个外角与它相邻内角的关系是(　　 )

A．互为余角　　 B．互为邻补角 C．两个角相等　　 D．外角大于内角

2. 如果一个多边形的边数增加一条，那么这个多边形的内角和增加　　　 ，外角和增加　　　 ．

1. 一个多边形的每一个外角都等于30°，则这个多边形为　　　 边形．

3.　　　 如果把六边形换成n边形．(n为不小于3的正整数)，n边形的外角和是多少？

由上面的探究可以得到：多边形的外角和等于_______.

所以我们说多边形的外角和与它的边数无关．

对此，我们也可以象以下这样理解为什么多边形的外角和等于360°．

如下图，从多边形的一个顶点A出发，沿多边形各边走过各顶点，再回到A点，然后转向出发时的方向，在行程中所转的各个角的和就是多边形的外角和，由于走了一周，所得的各个角的和等于一个周角，所以多边形的外角和等于360°．

活动3　课堂小结

　这节课你学到了哪些知识？学会了哪些方法？

活动4　课堂练习

2.如图，在六边形的每个顶点处各取一个外角，这些外角的和叫做六边形的外角和．六边形的外角和等于多少？

　 已知：∠1，∠2，∠3，∠4，∠5，∠6分别为六边形ABCDEF的外角．

求：∠1+∠2+∠3+∠4+∠5+∠6的值．

考虑以下问题

⑴任何一个外角同与它相邻的内角有什么关系？

⑵六边形的6个外角加上与它们相邻的内角，所得总和是多少？

⑶上述总和与六边形的内角和、外角和有什么关系？

联系这些问题，写出求外角和的过程.

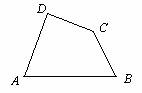
1.如果一个四边形的一组对角互补，那么另一组对角有什么关系？

已知：四边形ABCD的∠A+∠C＝180°．求：∠B与∠D的关系．

　　 (自主完成)

2.　　　 想一想：要得到多边形的内角和必需通过“三角形的内角和定理”来完成，就是把一个多边形分成几个三角形．除利用对角线把多边形分成几个三角形外，还有其他的分法吗？你会用新的分法得到n边形的内角和公式吗？

以五边形为例，由同学动手并推导，与同伴交流.

活动2　 简单应用