
2、提高学生观察、比较、归纳的能力,渗透类比的思维方法;
重点:掌握不等式的基本性质并能正确运用它们将不等式变形。
难点:掌握不等式的基本性质并能正确运用它们将不等式变形。
[情境设计]
复习:
1、了解不等式的意义,掌握不等式的基本性质,并能正确运用它们将不等式变形;
3.判断下列语句是否正确:
(1)若m<0,则5m>4m; ( )
(2)若x为有理数,则4x2 >-3x2; ( )
(3)若y为有理数,则4+y2>0; ( )
(4)若3a<-2a,则a<0; ( )
(5)若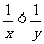 ,则x<y.
( )
,则x<y.
( )
2、有一个两位数,个位上的数字是a,十位上的数字是b,若把这个两位数的个位与十位数对调,得到的两位数大于原来的两位数,比较a与b的大小.
例1 设:a<b,用“<”或“>”号填空:
(1)a-3 b-3; (2)a-b 0.
(3)―4a ―4b; (4)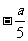
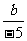 .
.
练习:课本P.14练习1
例2 根据不等式的性质,把下列不等式化为“x>a”或“x<a”的形式.
(1)x-4>3 (2)2x-3<x-2 (3)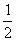 x+1>-3;
(4)-2x-4<4x+4; (5)
x+1>-3;
(4)-2x-4<4x+4; (5)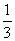 x≤
x≤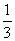 (x-2);
(x-2);
解:
练习:课本P.14练习2、习题7.3-1.2.3
注意:不等式的两边同乘以或除以同一个负数,不等号一定要改变方向.
总结本课的主要内容和注意点.
本课学习了不等式的两条基本性质,它是解不等式的理论基础.运用它们,我们能将不等式进行变形,但要注意不等式两边都乘以(或除以)同一个负数,不等号的方向改变.
拓展延伸:
1、(2005年.江西)已知a<2,则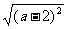 = .
= .
问:在解一元一次方程时,我们主要是对方程进行变形,那么方程变形主要有哪些?
答:去分母、移项、系数化为1.
问:这些解法具体步骤的主要依据是等式的两条基本性质.
等式基本性质1:在等式的两边都加上(或减去)同一个数或同一个整式,所得的结果仍是等式;
等式基本性质2:等式的两边都乘以或除以同一个数不等于0的数,所得的结果仍是等式
探索1:
(1)请同学们观察:课本P.12电梯里两人身高分别为:a米、b米,且a>b,都升高6米后的高度后的不等式关系:a+6>b+6;同理:a-3 b-3(填写“<”、“>”号
(2)实物演示:一个倾斜的天平两边分别放有重物,其质量分别为a和b(显然有a>b),如果在两边盘内再分别加上等量的砝码c,那么盘子会出现什么情况?
可让学生进行操作,并得出结论:盘子仍然像原来那样倾斜(即a+c>b+c).

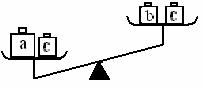
a>b  a+c>b+c.
a+c>b+c.
归纳1:
教师在学生得出结论的前提下总结:
不等式的性质1 不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.
用数学式了表示:
如果a>b, 那么a+c>b+c,a-c>b-c.
探索2:
问题: 如果不等式的两边都乘以(或除以)同一个不为零的数, 不等号的方向是否也不变呢?
将不等式7>4两边都乘以同一个数,比较所得数的大小,用“>”,“<”或“=”填空:
7×3 ______4×3,
7×2 ______4×2 ,
7×1______ 4×1,
……
7×(-1)______4×(-1),
7×(-2)______4×(-2),
7×(-3)______4×(-3),
……
从中你能发现什么?在学生所得出的结论的基础上,引导学生总结概括出不等式的另外一条性质.
不等式的性质2 不等式的两边都乘(或除以)同一个正数,不等号的方向不变;不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
用数学式了表示:
如果a>b,并且c>0,那么ac>bc.; 如果a>b,并且c<0,那么ac<bc.
思考:不等式的两边都乘0,结果又怎样?
如:7 4 而 7×0______ 4×0.
不等式的性质与等式的性质比较如下表:
|
等式的性质 |
不等式的性质 |
|
1. 如果a=b,那么 a+c=b+c, a―c=b―c |
1. 如果a>b,那么 a+c>b+c, a―c>b―c |
|
2. 如果a=b,且c≠0, 那么 ac=bc, 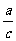 = = 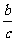 |
2.
如果a>b,且c>0, 那么ac>bc, 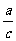 > >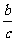 ; ;如果a>b,且c<0, 那么ac<bc, 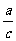 < <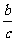 . . |
注意:不等式两边都乘以(或除以)同一个负数,不等号的方向改变.
课本第14页习题7.3第1、2题;
2.你能把不等式-1>x变形为x<-1吗?为什么?
1.将不等式2 x>4x的两边都除以x,得2>4。你认为对吗?如果不对,错在哪呢?
4.已知x<2,能否推出3-2x>-1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com